
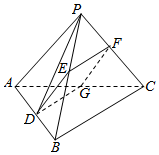
 在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.
在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.分析 (1)由已知得EF∥BC,从而BC∥平面EFG.从而DG∥BC.由此得到AD=DB,从而能证明点D是线段AB的中点.
(2)连PG,由(1)知DG∥BC,∠PDG的大小等于异面直线PD与BC所成角的大小或其补角的大小,由此能求出异面直线PD与BC所成的角大小.
解答 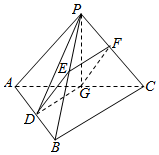 证明:(1)∵PE=EB,PF=FC,∴EF∥BC,
证明:(1)∵PE=EB,PF=FC,∴EF∥BC,
∴BC∥平面EFG.
又由BC∥平面EFG,过BC作平面ABC与平面EFG相交交线为DG,
则DG∥BC.
∵AG=GC,∴AD=DB,点D是线段AB的中点.…(4分)
解:(2)连PG,由(1)知DG∥BC,
∠PDG的大小等于异面直线PD与BC所成角的大小或其补角的大小.…(6分)
在△PDG中,DG=3,$PD=PG=\sqrt{{5^2}-{3^2}}=4$,
$cos∠PDG=\frac{1.5}{4}=\frac{3}{8}$,$∠PDG=arccos\frac{3}{8}$.
∴异面直线PD与BC所成的角大小等于$arccos\frac{3}{8}$.…(8分)
点评 本题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
| 编号 位置 | ① | ② | ③ | ④ |
| 山上 | 5.0 | 3.8 | 3.6 | 3.6 |
| 山下 | 3.6 | 4.4 | 4.4 | 3.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2+x3>0 | B. | x1+x2+x3=0 | ||
| C. | x1+x2+x3<0 | D. | x1+x2+x3的符号不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com