
分析 (1)y=2cos2x+4asinx+a-3=2a2+a-1-2(sinx-a)2,分类讨论,当-1≤a≤1时,函数最大值M(a)=2a2+a-1,当a<-1时,函数最大值M(a)=2a2+a-1-2 (-1-a)2=-3a-3; 当a>1时,函数最大值M(a)=2a2+a-1-2 (1-a)2=5a-3.代入求得a的值.
(2)令 sinx=t,由0≤x≤π,得0≤sinx≤1,由题意可得g(t)=2a2+a-1-2(t-a)2,的图象在[0,1)上与横轴.
解答 解:(1)y=2cos2x+4asinx+a-3
=2a2+a-1-2(sinx-a)2,
当-1≤a≤1时,函数最大值M(a)=2a2+a-1,f(x)的最大值为1,
∴a=$\frac{-1+\sqrt{17}}{4}$;
当a<-1时,函数最大值M(a)=2a2+a-1-2(-1-a)2=-3a-3,f(x)的最大值为1,
∴a=$-\frac{4}{3}$,
当a>1时,函数最大值M(a)=2a2+a-1-2(1-a)2=5a-3,f(x)的最大值为1,
a=$\frac{4}{5}$(舍去);
(2)若f(x)=0在[0,π]上有2个解,令 sinx=t,
∵0≤x≤π,
∴0≤sinx≤1,
∴0≤t≤1.
由于当t在[0,1)上任意取一个值,x在[0,π)]上都有2个值与之对应,
当t=1时,只有一个x=$\frac{π}{2}$与之对应.
故由题意f(x)=0在[0,π]有2个解,
可得关于t的函数 g(t)=2a2+a-1-2(t-a)2 =-2t2+4at+a-1,
∴g(x)的图象在[0,1)上,与横轴只能有一个交点,
即关于t的方程 g(t)=0在[0,1)上有唯一解.
∴$\left\{\begin{array}{l}{△=16{a}^{2}+8a-8=0}\\{0≤a<1}\\{g(0)≤0}\\{g(1)≤0}\end{array}\right.$,$\left\{\begin{array}{l}{a=\frac{1}{2}或a=-1}\\{0<a<1}\\{a-1≤0}\\{5a-3<0}\end{array}\right.$,
即a=$\frac{1}{2}$,
故a的取值范围是{$\frac{1}{2}$}.
点评 本题考查同角三角函数的基本关系,二次函数的最值问题,令 sinx=t,判断g(t)=2a2+a-1-2(t-a)2,在[0,1]上,与横轴有两个交点,是解题的关键,属于中档题.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
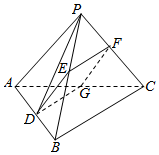 在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.
在四面体PABC中,PA=PB=PC=5,AB=BC=AC=6,点E、F、G都是所在边的中点,E、F、G这三点所确定的平面与直线AB相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com