
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用两角和差的正弦余弦正切公式进行排除.
解答 解:对于任意的角α,β,使得cos(α+β)=cosαcosβ-sinαsinβ成立,故①错,
对任意的角α,β,sin(α+β)=sinαcosβ+cosαsinβ成立;故②错,
sinαsinβ=1,
∴sinα=sinβ=1或sinα=sinβ=-1,
∴cos(α+β)=±1,故③错,
对于α≠$kπ+\frac{π}{2}$,β≠$kπ+\frac{π}{2}$,使得tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$成立.故④错,
故答案选:A.
点评 本题考查两角和差的正弦余弦正切公式及适用条件,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
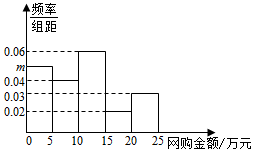 某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图
某调查机构从某县农村淘宝服务网点中随机抽取20个网点作为样本进行元旦期间网购金额(单位:万元)的调查.获得的所有样本数据按照区间[0,5],(5,10],(10,15],(15,20],(20,25]进行分组,得到如图所示的频率直方图查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com