
(2014•镇江二模)已知不等式|a﹣2|≤x2+2y2+3z2对满足x+y+z=1的一切实数x,y,z都成立,求实数a的取值范围.
科目:高中数学 来源:[同步]2014年新人教A版选修4-6 1.1整除练习卷(解析版) 题型:填空题
(2013•宝山区一模)我们用记号“|”表示两个正整数间的整除关系,如3|12表示3整除12.试类比课本中不等关系的基本性质,写出整除关系的两个性质.① ;② .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 4.1数学归纳法练习卷(解析版) 题型:选择题
证明1+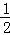
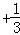
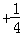 +…+
+…+
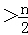 (n∈N*),假设n=k时成立,当n=k+1时,左端增加的项数是( )
(n∈N*),假设n=k时成立,当n=k+1时,左端增加的项数是( )
A.1项 B.k﹣1项 C.k项 D.2k项
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷(解析版) 题型:填空题
(2014•辽宁)对于c>0,当非零实数a,b满足4a2﹣2ab+b2﹣c=0且使|2a+b|最大时, +
+ +
+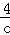 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷(解析版) 题型:填空题
(2014•长安区三模)己知x,y∈(0,+∞),若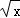 +3
+3 <k
<k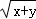 恒成立,利用柯西不等式可求得实数k的取值范围是 .
恒成立,利用柯西不等式可求得实数k的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷(解析版) 题型:选择题
已知a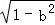 +b
+b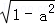 =1,则以下成立的是( )
=1,则以下成立的是( )
A.a2+b2>1 B.a2+b2=1 C.a2+b2<1 D.a2b2=1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷(解析版) 题型:选择题
用反证法证明“方程ax2+bx+c=0(a≠0)至多有两个解”的假设中,正确的是( )
A.至多有一个解 B.有且只有两个解
C.至少有三个解 D.至少有两个解
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-5 2.1比较法练习卷(解析版) 题型:选择题
若不等式(﹣1)na<2+ 对任意n∈N*恒成立,则实数a的取值范围是( )
对任意n∈N*恒成立,则实数a的取值范围是( )
A.[﹣2, ) B.(﹣2,
) B.(﹣2, ) C.[﹣3,
) C.[﹣3, ) D.(﹣3,
) D.(﹣3, )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com