
 ,则给出下列四个命题:①函数
,则给出下列四个命题:①函数 的定义域是R,值域为[0,1];②方程
的定义域是R,值域为[0,1];②方程 有无数个解;③函数
有无数个解;③函数 是周期函数;④函数
是周期函数;④函数 是增函数.其中正确的序号是 ( )
是增函数.其中正确的序号是 ( )| A.①③ | B.②④ | C.①④ | D.②③ |
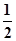 时,{x}=
时,{x}=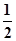 ,又∵函数{x}=x-[x]是周期为1的函数,∴x=
,又∵函数{x}=x-[x]是周期为1的函数,∴x=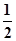 +k时(k∈Z),{x}=
+k时(k∈Z),{x}=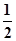 ,∴②是正确的,
,∴②是正确的,

科目:高中数学 来源:不详 题型:填空题
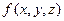 满足
满足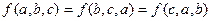 ,则称函数
,则称函数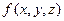 为轮换对称函数,如
为轮换对称函数,如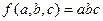 是轮换对称函数,下面命题正确的是
是轮换对称函数,下面命题正确的是 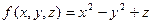 不是轮换对称函数.
不是轮换对称函数.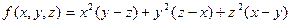 是轮换对称函数.
是轮换对称函数.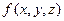 和函数
和函数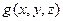 都是轮换对称函数,则函数
都是轮换对称函数,则函数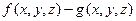 也是轮换对称函数.
也是轮换对称函数.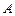 、
、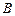 、
、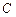 是
是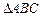 的三个内角, 则
的三个内角, 则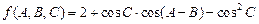 为轮换对称函数.
为轮换对称函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com