
【题目】如图所示,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见详解;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接OF,可得OF为![]() 的中位线,OF∥DE,可得证明;
的中位线,OF∥DE,可得证明;
(2)连接C点与AD中点为x轴,CB为y轴,CE为z轴建立空间直角坐标系,可得![]() ,
,![]() 的值,可得异面直线
的值,可得异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)可得平面EBD的一个法向量为![]() ,可得
,可得![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)
如图,连接OF,因为底面![]() 是菱形,
是菱形,![]() 与
与![]() 交于点
交于点![]() ,
,
可得O点为BD的中点,又![]() 为
为![]() 的中点,所以OF为
的中点,所以OF为![]() 的中位线,
的中位线,
可得OF∥DE,又![]() ,DE不在平面ACF内,
,DE不在平面ACF内,
可得![]() 平面
平面![]() ;
;
(2)如图连接C点与AD中点位x轴,CB为y轴,CE为z轴建立空间直角坐标系,
设菱形![]() 的边长为2,可得CE=2,
的边长为2,可得CE=2,
可得E(0,0,2),O(![]() ,
,![]() ,0),A(
,0),A(![]() ,1,0),F(0,1,1),
,1,0),F(0,1,1),
可得:![]() ,
,![]() ,设异面直线
,设异面直线![]() 与
与![]() 所成角为
所成角为![]() ,
,
可得 ,
,
(3)可得D (![]() ,-1,0),B(0,2,0),E(0,0,2),
,-1,0),B(0,2,0),E(0,0,2),
可得![]() ,
,![]() ,设平面EBD的一个法向量为
,设平面EBD的一个法向量为![]() ,
,
可得![]() ,
,![]() ,可得
,可得![]() 的值可为
的值可为![]() ,由
,由![]()
可得![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为
 =
= .
.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() :
:![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 上的所有点的横坐标缩短为原来的
上的所有点的横坐标缩短为原来的![]() ,纵坐标缩短为原来的
,纵坐标缩短为原来的![]() 后得到曲线
后得到曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为 。
。
(1)求曲线![]() 的极坐标方程和直线l的直角坐标方程;
的极坐标方程和直线l的直角坐标方程;
(2)设直线l与曲线![]() 交于不同的两点A,B,点M为抛物线
交于不同的两点A,B,点M为抛物线![]() 的焦点,求
的焦点,求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有除颜色外形状大小完全相同的6个小球,其中有4个编号为1,2, 3, 4的红球,2个编号为A、B的黑球,现从中任取2个小球.;
(1)求所取2个小球都是红球的概率;
(2)求所取的2个小球颜色不相同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
(1)求![]() 的值;
的值;
(2)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
类舒适型轿车中抽取8辆,经检测它们的得分如下:4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
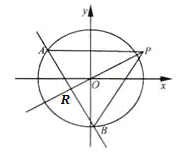
【题目】如图,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为![]() .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 求![]() ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() (其中
(其中![]() 为顶点,
为顶点,![]() 为底面圆心)的侧面积与底面积的比是
为底面圆心)的侧面积与底面积的比是![]() ,则圆锥
,则圆锥![]() 与它的外接球(即顶点在球面上且底面圆周也在球面上)的体积比为__________.
与它的外接球(即顶点在球面上且底面圆周也在球面上)的体积比为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】食品安全问题越来越引起人们的重视,农药、化肥的滥用对人民群众的健康带来一定的危害,为了给消费者带来放心的蔬菜,某农村合作社每年投入200万元,搭建了甲、乙两个无公害蔬菜大棚,每个大棚至少要投入20万元,其中甲大棚种西红柿,乙大棚种黄瓜,根据以往的种菜经验,发现种西红柿的年收入![]() 种黄瓜的年收入
种黄瓜的年收入![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]() .设甲大棚的投入为
.设甲大棚的投入为![]() (单位:万元),每年两个大棚的总收益为
(单位:万元),每年两个大棚的总收益为![]() (单位:万元)
(单位:万元)
(1)求![]() 的值;
的值;
(2)试问如何安排甲、乙两个大棚的投入,才能使总收益![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com