
| A. | (-∞,0) | B. | (-1,1) | C. | (0,1) | D. | (-∞,1),(0,1) |
分析 利用导函数研究f(x)的单调性可得答案.
解答 解:函数f(x)=2x3-ax+6,
则f′(x)=6x2-a,
当a≤0时,f′(x)≥0恒成立,函数f(x)在其定义域内是递增.
当a>0时,令f′(x)=0,
解得:x=$±\sqrt{\frac{a}{6}}$,
当x在($\sqrt{\frac{a}{6}}$,+∞)时,f′(x)>0,函数f(x)是递增.
∵函数f(x)的一个单调递增区间为[1,+∞),
故得:$\sqrt{\frac{a}{6}}$=1,
解得:a=6,
∴x在(-1,1)时,f′(x)<0,函数f(x)是递减.
故选B.
点评 本题考查了利用导函数研究函数的单调性问题.属于中档题.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
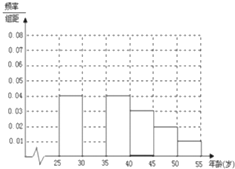 某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):
某班同学参加社会实践活动,对本市25~55岁年龄段的人群进行某项随机调查,得到各年龄段被调查人数的频率分布直方图如右(部分有缺损):查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{160π}{3}$ | B. | $\frac{59π}{6}$ | C. | $\frac{325π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com