
分析 (1)求出函数的导数,通过讨论a的范围,即可求解a的值.
(2)求出g′(x),列出求解函数的极值点的方程,利用韦达定理,化简g(x1)-g(x2),构造新函数,通过新函数的导数求解函数的最值.
解答 解:(1)∵f(x)=x+alnx,(x>0),
∴f′(x)=1+$\frac{a}{x}$=$\frac{x+a}{x}$
a≥0时,f′(x)>0,函数在(0,+∞)递增;
a<0时,令f′(x)=0,解得:x=-a,
∴f(x)在(0,-a)递减,在(-a,+∞)递增;
(2)a=1时:g(x)=x+lnx+$\frac{1}{2}$x2-bx,
g′(x)=$\frac{1}{x}$+x-(b-1)=$\frac{{x}^{2}-(b-1)x+1}{x}$,
令g′(x)=0,得x2-(b-1)x+1=0,∴x1+x2=b-1,x1x2=1,
∵g(x1)-g(x2)=[lnx1+$\frac{1}{2}$${{x}_{1}}^{2}$-(b-1)x1]-[lnx2+$\frac{1}{2}$${{x}_{2}}^{2}$-(b-1)x2]
=ln $\frac{{x}_{1}}{{x}_{2}}$+$\frac{1}{2}$(${{x}_{1}}^{2}$-${{x}_{2}}^{2}$)-(b-1)(x1-x2)=ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{1}{2}$($\frac{{x}_{1}}{{x}_{2}}$-$\frac{{x}_{2}}{{x}_{1}}$),
∵0<x1<x2,所以设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),
h(t)=lnt-$\frac{1}{2}$(t-$\frac{1}{t}$)(0<t<1),
h′(t)=$\frac{1}{t}$-$\frac{1}{2}$(1+$\frac{1}{{t}^{2}}$)=-$\frac{{(t-1)}^{2}}{{2t}^{2}}$<0,
所以h(t)在(0,1)单调递减,
又b≥$\frac{7}{2}$,∴(b-1)2≥$\frac{25}{4}$,
即(x1+x2)2=$\frac{{{(x}_{1}+{x}_{2})}^{2}}{{x}_{1}{•x}_{2}}$=t+$\frac{1}{t}$+2≥$\frac{25}{4}$,
∵0<t<1,∴4t2-17t+4≥0,∴0<t≤$\frac{1}{4}$,
∴h(t)≥h($\frac{1}{4}$)=$\frac{15}{8}$-2ln2,
故所求的最小值是$\frac{15}{8}$-2ln2.
点评 本题考查函数的导数的应用,函数的极值的求法韦达定理以及构造法的应用,考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y+1)2=2 | B. | (x+2)2+(y-1)2=4 | C. | (x-2)2+(y+1)2=8 | D. | (x+2)2+(y-1)2=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c,d | B. | d,e | C. | b,e | D. | c,e |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
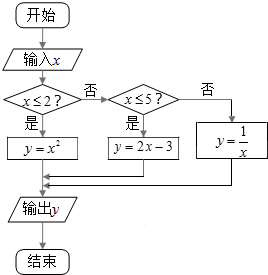 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com