
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为5.
的距离为5.
(1)求![]() 与
与![]() 的值;
的值;
(2)设动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在与
轴上是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】陕西关中的秦腔表演朴实,粗犷,细腻,深刻,再有电子布景的独有特效,深得观众喜爱.戏曲相关部门特意进行了“喜爱看秦腔”调查,发现年龄段与爱看秦腔的人数比存在较好的线性相关关系,年龄在![]() ,
,![]() ,
,![]() ,
,![]() 的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表
的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表![]() .由此求得爱看人数比
.由此求得爱看人数比![]() 关于年龄段
关于年龄段![]() 的线性回归方程为
的线性回归方程为![]() .那么,年龄在
.那么,年龄在![]() 的爱看人数比为( )
的爱看人数比为( )
A.0.42B.0.39C.0.37D.0.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
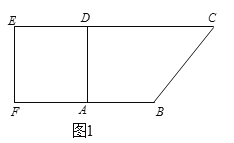
【题目】如图1,在直角梯形![]() 中,AB∥CD,
中,AB∥CD,![]() ,且
,且![]() .现以
.现以![]() 为一边向梯形外作正方形
为一边向梯形外作正方形![]() ,然后沿边
,然后沿边![]() 将正方形
将正方形![]() 翻折,使平面
翻折,使平面![]() 与平面
与平面![]() 垂直,如图2.
垂直,如图2.
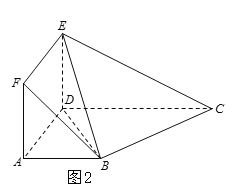
(Ⅰ)求证:BC⊥平面DBE;
(Ⅱ)求点D到平面BEC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
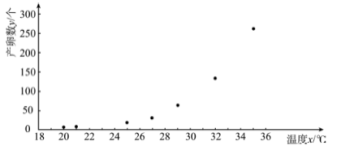
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在制造产品时需要用到长度为698mm的A型和长度为518mm的B型两种钢管,工厂利用长度为4000mm的钢管原材料,裁剪成若干A型和B型钢管。假设裁剪时损耗忽略不计,裁剪后所剩废料与原材料的百分比称为废料率.
(1)有两种裁剪方案的废料率小于4.5%,请说明这两种方案并计算它们的废料率;
(2)工厂现有100根原材料钢管,一根A型和一根B型钢管为一套毛胚。按(1)中的方案裁剪,最多可裁剪多少套毛胚?最终的废料率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com