
分析 计算${\overrightarrow{b}}^{2}$,将x=2-2y代入得到关于y的函数,求此函数的最小值.
解答 解:$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=cos$\frac{π}{3}$=$\frac{1}{2}$.$\overrightarrow{b}$2=x2+y2+2xy$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=x2+y2+xy.
∵x+2y=2,∴x=2-2y.
∴$\overrightarrow{b}$2=(2-2y)2+y2+(2-2y)y=3y2-6y+4=3(y-1)2+1.
∴当y=1时,$\overrightarrow{b}$2取得最小值1.
∴|$\overrightarrow{b}$|的最小值为1.
故答案为:1.
点评 本题考查了平面向量数量积的运算,二次函数的最值,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-∞,1)∪(2,+∞) | C. | (-∞,2) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\frac{{\sqrt{3}}}{3}]$ | B. | $(0,\sqrt{3}]$ | C. | $[0,\frac{{\sqrt{3}}}{3}]$ | D. | $[0,\sqrt{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
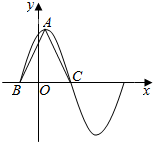 函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
函数f(x)=2$\sqrt{3}$sin(ωx+$\frac{π}{3}$)(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -8 | B. | -10 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 5 | C. | 7 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):
2015年7月9日21时15分,台风“莲花”在我国广东省陆丰市甲东镇沿海登陆,造成165.17万人受灾,5.6万人紧急转移安置,288间房屋倒塌,46.5千公顷农田受灾,直接经济损失12.99亿元.距离陆丰市222千米的梅州也受到了台风的影响,适逢暑假,小明调查了梅州某小区的50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,并作出如下频率分布直方图(如图):| 经济损失不超过4000元 | 经济损失超过4000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com