
【题目】甲船在点![]() 发现乙船在北偏东
发现乙船在北偏东![]() 的
的![]() 处,
处,![]() 里,且乙船以每小时10里的速度向正北行驶,已知甲船的速度是每小时
里,且乙船以每小时10里的速度向正北行驶,已知甲船的速度是每小时![]() 里,问:甲船以什么方向前进,才能与乙船最快相遇,相遇时甲船行驶了多少小时?
里,问:甲船以什么方向前进,才能与乙船最快相遇,相遇时甲船行驶了多少小时?

【答案】甲船应朝北偏东30°方向行驶,才能与乙船最快相遇,相遇时甲船行驶了2小时.
【解析】
构建两个直角三角形后,在RT△ABD,可求出AD,BD,设![]() ,在RT△ACD中运用勾股定理可求出
,在RT△ACD中运用勾股定理可求出![]() ,从而求出∠CAD,则可找到甲船所行驶方向,进而求出相遇时的时间.
,从而求出∠CAD,则可找到甲船所行驶方向,进而求出相遇时的时间.
解:如图,设甲船在C处追上乙船,延长CB与东西方向交与点D,根据题意知CD⊥AD,
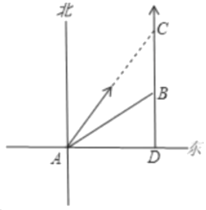
∴∠ADB=90°,∠BAD=30°,![]()
∴BD=10,
由勾股定理得:AD=![]() ,
,
∵乙船正以每小时10海里的速度向正北方向行驶,而甲船的速度是![]() 海里/小时,
海里/小时,
∴设![]() ,则AC=
,则AC=![]() ,
,
又在![]() 中,
中,![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
此时AC=![]() ,
,![]() ,
,
所以![]() ,
,
相遇时甲船行驶了![]() 小时,
小时,
∴甲船应朝北偏东30°方向行驶,才能与乙船最快相遇,相遇时甲船行驶了2小时,
故答案为:甲船应朝北偏东30°方向行驶,才能与乙船最快相遇,相遇时甲船行驶了2小时.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() ,在某一周期内的图象时,列表并填入了部分数据,如下表:
,在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
x |
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,并求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调递增区间;
的单调递增区间;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)记函数![]() 的导函数是
的导函数是![]() ,若不等式
,若不等式![]() 对任意的实数
对任意的实数![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)设函数![]() ,
,![]() 是函数
是函数![]() 的导函数,若函数
的导函数,若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月26日,铁人中学举行了盛大的成人礼.仪式在《相信我们会创造奇迹》的歌声中拉开序幕,庄严而神圣的仪式感动了无数家长,4月27日,铁人中学官方微信发布了整个仪式精彩过程,几十年众志成城,数十载砥砺奋进,铁人中学正在创造着一个又一个奇迹.官方微信发布后,短短几个小时点击量就突破了万人,收到了非常多的精彩留言.学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(Ⅰ)求这100位留言者年龄的样本平均数![]() 和样本方差
和样本方差![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(Ⅱ)由频率分布直方图可以认为,留言者年龄![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本均数
近似为样本均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(ⅰ)利用该正态分布,求![]() ;
;
(ii)学校从年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间
的留言者中,按照分层抽样的方法,抽出了7人参加“精彩留言”表彰大会,现要从中选出3人作为代表发言,设这3位发言者的年龄落在区间![]() 的人数是
的人数是![]() ,求变量
,求变量![]() 的分布列和数学期望.附:
的分布列和数学期望.附:![]() ,若
,若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.

(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H关于t的函数解析式;
(2)求游客甲在开始转动5min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在已分组的若干数据中,每组的频数是指___________,每组的频率是指____________.
(2)一个公司共有N名员工,下设一些部门,要采用等比例外层随机抽样的方法从全体员工中抽取样本量为n的样本,如果某部门有m名员工,那么从该部门抽取的员工人数是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(![]() 分成六段:
分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,统计后得到如图的频率分布直方图.
,统计后得到如图的频率分布直方图.
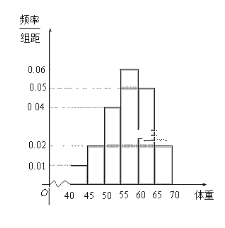
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在![]() 的同学中任意抽取3位,求体重在
的同学中任意抽取3位,求体重在![]() ,
,![]() 内都有同学的概率.
内都有同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com