
分析 根据三角函数的单调性列出不等式解出单调区间,然后与定义域取交集即可.
解答 解:(1)令$\frac{π}{2}+2kπ≤$x+$\frac{π}{4}$≤$\frac{3π}{2}+2kπ$,解得$\frac{π}{4}+2kπ≤x≤\frac{5π}{4}+2kπ$.
当k=-1时,函数的递减区间为[-$\frac{7π}{4}$,-$\frac{3π}{4}$],当k=0时,函数的递减区间为[$\frac{π}{4}$,$\frac{5π}{4}$].
∴函数在[-π,π]上的递减区间为[-π,-$\frac{3π}{4}$],[$\frac{π}{4}$,π].
(2)令-π+2kπ≤$\frac{1}{2}x+\frac{2π}{3}$≤2kπ,解得-$\frac{10π}{3}+4kπ$≤x≤-$\frac{4π}{3}+4kπ$.
当k=1时,函数的单调增区间是[$\frac{2π}{3}$,$\frac{8π}{3}$].
∴函数在[0,2π]上的递增区间是[$\frac{2π}{3}$,2π].
(3)令-$\frac{π}{2}+2kπ$≤3x-$\frac{π}{6}$≤$\frac{π}{2}+2kπ$,解得-$\frac{π}{9}$+$\frac{2kπ}{3}$≤x≤$\frac{2π}{9}+\frac{2kπ}{3}$.
∴函数的递增区间是[-$\frac{π}{9}$+$\frac{2kπ}{3}$,$\frac{2π}{9}+\frac{2kπ}{3}$],k∈Z.
点评 本题考查了三角函数的图象与性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-\sqrt{13}}{2}$ | B. | $\frac{3+\sqrt{13}}{2}$ | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
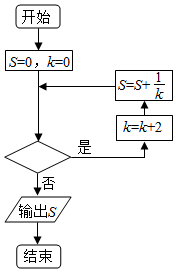 执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )
执行如图所示的程序框图,若输出的S=$\frac{25}{24}$,则判断框内填入的条件可以是( )| A. | k≥7 | B. | k>7 | C. | k≤8 | D. | k<8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com