
分析 (1)由a1=1,利用递推公式能求出a2,a3,a4,a5的值.
(2)由题意,对于任意的正整数n,bn=${a}_{{2}^{n-1}}$+1,从而bn+1=${a}_{{2}^{n}}$+1,进而bn+1=2bn,由此能证明数列{bn}是首项、公比均为2的等比数列,并求出其通项公式.
(3)对任意的m≥2,m∈N*,在数列{an}中存在连续的2m项构成等差数列.对任意的m≥2,k∈N*,在数列{an}中,${a}_{{2}^{m}}$,${a}_{{2}^{m}+1}$,${a}_{{2}^{m}+2}$,…,${a}_{{2}^{m}+{2}^{m}-1}$这连续的2m就构成一个等差数列.利用构造法和分类讨论法能推导出${a}_{{2}^{m}}$,${a}_{{2}^{m}+1}$,${a}_{{2}^{m}+2}$,…,${a}_{{2}^{m}+{2}^{m}-1}$这连续的2m项,是首项为${a}_{{2}^{m}}={2}^{m+1}-1$,公差为-$\frac{1}{2}$的等差数列.
解答 解:(1)∵a1=1,∴a2=1+2a1=3,
a3=$\frac{1}{2}$+2a2=$\frac{5}{2}$,
a4=1+2a3=7,
a5=$\frac{1}{2}$+2a4=$\frac{13}{2}$;
证明:(2)由题意,对于任意的正整数n,bn=${a}_{{2}^{n-1}}$+1,
∴bn+1=${a}_{{2}^{n}}$+1,
又∵${a}_{{2}^{n}}$+1=(2${a}_{\frac{{2}^{n}}{2}}$+1)+1=2(${a}_{{2}^{n-1}}$+1)=2bn,
∴bn+1=2bn,
又∵b1=${a}_{{2}^{1-1}}$+1=a1+1=2,
∴数列{bn}是首项、公比均为2的等比数列,其通项公式bn=2n;
(3)对任意的m≥2,m∈N*,在数列{an}中存在连续的2m项构成等差数列.
对任意的m≥2,k∈N*,在数列{an}中,${a}_{{2}^{m}}$,${a}_{{2}^{m}+1}$,${a}_{{2}^{m}+2}$,…,${a}_{{2}^{m}+{2}^{m}-1}$这连续的2m就构成一个等差数列.
我们先来证明:“对任意的n≥2,n∈N*,k∈(0,2n-1),k∈N*,有${a}_{{2}^{n-1}+k}={2}^{n}-1-\frac{k}{2}$”,
由(2)得${b}_{n}={a}_{{2}^{n-1}}+1={2}^{n}$,∴${a}_{{2}^{n-1}}={2}^{n}-1$,
当k为奇数时,${a}_{{2}^{n-1}+k}=\frac{1}{2}+2{a}_{\frac{{2}^{n-1}+k-1}{2}}$=$\frac{1}{2}+2{a}_{{2}^{n-2}+\frac{k-1}{2}}$,
当k为偶数时,${a}_{{2}^{n-1}+k}=1+2{a}_{\frac{{2}^{n-1}+k}{2}}$=1+2a${\;}_{{2}^{n-2}+\frac{k}{2}}$,
记${k}_{1}=\left\{\begin{array}{l}{\frac{k}{2},k为偶数}\\{\frac{k-1}{2},k为奇数}\end{array}\right.$,∴要证${a}_{{2}^{n-2}+{k}_{1}}$=${2}^{n}-1-\frac{k}{2}$,只需证明${a}_{{2}^{n-2}+{k}_{1}}={2}^{n-1}-1-\frac{{k}_{1}}{2}$,
其中${k}_{1}∈(0,{2}^{n-2})$,k1∈N*,
(这是因为若${a}_{{2}^{n-2}}={2}^{n-1}-1-\frac{{k}_{1}}{2}$,则当${k}_{1}=\frac{k-1}{2}$时,则k一定是奇数)
有${a}_{{2}^{n-1}+k}=\frac{1}{2}+2{a}_{\frac{{2}^{n-1}+k-1}{2}}$=$\frac{1}{2}+2{a}_{{2}^{n-2}+\frac{k-1}{2}}$
=$\frac{1}{2}+2({2}^{n-1}-1-\frac{{k}_{1}}{2})=\frac{1}{2}+2({2}^{n-1}-1-\frac{\frac{k-1}{2}}{2})$=${2}^{n}-1-\frac{k}{2}$,
当${k}_{1}=\frac{k}{2}$时,则k一定是偶数,
有${a}_{{2}^{n-1}+k}=1+2{a}_{\frac{{2}^{n-1}+k}{2}}$=1+$2{a}_{{2}^{n-1}+\frac{k}{2}}$
=1+2(${2}^{n-1}-1-\frac{{k}_{1}}{2}$)=1+2(${2}^{n-1}-1-\frac{\frac{k}{2}}{2}$)=${2}^{n}-1-\frac{k}{2}$,
以此递推,要证${a}_{{2}^{n-2}+{k}_{1}}$=${2}^{n-1}-1-\frac{{k}_{1}}{2}$,只要证明${a}_{{2}^{n-3}+{k}_{2}}={2}^{n-2}-1-\frac{{k}_{2}}{2}$,
其中${k}_{2}=\left\{\begin{array}{l}{\frac{{k}_{1}}{2},{k}_{1}为偶数}\\{\frac{{k}_{1}-1}{2},{k}_{1}为奇数}\end{array}\right.$,k2∈N*,
如此递推下去,我们只需证明${a}_{{2}^{l}+{k}_{n-2}}={2}^{2}-1-\frac{{k}_{n-2}}{2}$,${k}_{n-2}∈(0,{2}^{l}),{k}_{n-2}∈{N}^{*}$,
即${a}_{{2}^{l}+1}={2}^{2}-1-\frac{1}{2}=3-\frac{1}{2}=\frac{5}{2}$,即${a}_{3}=\frac{5}{2}$,
由(Ⅱ)可得,所以对n≥2,n∈N*,k∈(0,2n-1),k∈N*,
有${a}_{{2}^{l}+1}={2}^{n}-1-\frac{k}{2}$,
对任意的m≥2,m∈N*,
${a}_{{2}^{m}+i}$=${2}^{m+1}-1-\frac{i}{2}$,${a}_{{2}^{m}+i+1}={2}^{m+1}-1-\frac{i+1}{2}$,其中i∈(0,2m-1),i∈N*,
∴${a}_{{2}^{m}+i+1}$-${a}_{{2}^{m}+i}$=-$\frac{1}{2}$,
又${a}_{{2}^{m}+1}-1$,${a}_{{2}^{m}+1}={2}^{m+1}-1-\frac{1}{2}$,
∴${a}_{{2}^{m}+1}-{a}_{{2}^{m}}=-\frac{1}{2}$,
∴${a}_{{2}^{m}}$,${a}_{{2}^{m}+1}$,${a}_{{2}^{m}+2}$,…,${a}_{{2}^{m}+{2}^{m}-1}$这连续的2m项,是首项为${a}_{{2}^{m}}={2}^{m+1}-1$,公差为-$\frac{1}{2}$的等差数列.
点评 本题考查数列的前5项的求法,考查等比数列的证明及通项公式的求法,考查满足条件等差数列是否存在的判断与求法,考查推理论证能力、运算求解能力,考查分类与整合思想、化归与转化思想、函数与方程思想,是难题.


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
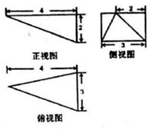 某几何体的三视图如图所示,则该几何体中最长的棱长为( )
某几何体的三视图如图所示,则该几何体中最长的棱长为( )| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{21}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{b}{a}$ | D. | $\frac{a}{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{9}{2}$π+24 | B. | $\frac{9}{2}$π+30 | C. | 9π+54 | D. | 36π+30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com