
设f(x)是(-∞,+∞)上的奇函数,f(x+2)=-f(x),当0≤x≤1时,f(x)=x.
(1)求f(π)的值;
(2)当-4≤x≤4时,求f(x)的图象与x轴所围图形的面积.
 解析:(1)由f(x+2)=-f(x),得
解析:(1)由f(x+2)=-f(x),得
f(x+4)=f[(x+2)+2]=-f(x+2)=f(x),
所以f(x)是以4为周期的函数,从而得
f(π)=f(-1×4+π)=f(π-4)=-f(4-π)=-(4-π)=π-4.
(2)由f(x)是奇函数与f(x+2)=-f(x),得f[(x-1)+2]=-f(x-1)=f[-(x-1)],
即f(1+x)=f(1-x).
故知函数y=f(x)的图象关于直线x=1对称.
又0≤x≤1时,f(x)=x,且f(x)的图象关于原点成中心对称,则f(x)的图象如图所示.
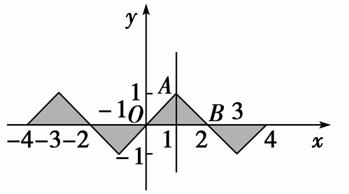
当-4≤x≤4时,f(x)的图象与x轴围成的图形面积为S,
则S=4S△OAB=4×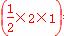 =4.
=4.


科目:高中数学 来源: 题型:
一个无盖的正方体盒子展开后的平面图如图所示,A、B、C是展开图上的三点,则在正方体盒子中,∠ABC的大小为( )

A.30°  B.45°
B.45°
C.60° D.9 0°
0°
查看答案和解析>>
科目:高中数学 来源: 题型:
如图是函数f(x)的图象,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数f(x)零点的区间是( )

A.[-2.1,-1] B.[1.9,2.3]
C.[4.1,5] D.[5,6.1]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com