
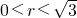 ),记点P的轨迹的长度为f(r),则
),记点P的轨迹的长度为f(r),则 =________.(填上所有可能的值).
=________.(填上所有可能的值).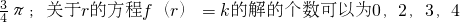
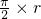 =
=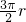 ;∴
;∴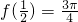 .此时,由一次函数的单调性可得:
.此时,由一次函数的单调性可得: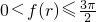 <5.
<5.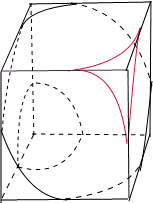
 时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则
时,在平面ABCD内,设以点A为圆心,r为半径的圆弧与BC、CD分别交于点E、F,则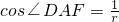 ,
,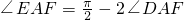 ,
,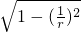 ×
×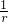 =
=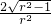 ,cos∠EAG=
,cos∠EAG=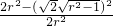 =
= ,
,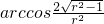 +3r
+3r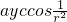 ;
; 时,∵CM=
时,∵CM= ,∴
,∴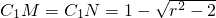 ,∴cos∠MAN=
,∴cos∠MAN=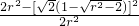 =
=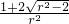 ,
,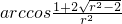 .
.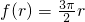 ;当1<r≤
;当1<r≤ 时,f(r)=3r
时,f(r)=3r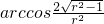 +3r
+3r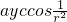 ;当
;当 时,∴f(r)=3r
时,∴f(r)=3r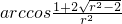 .
.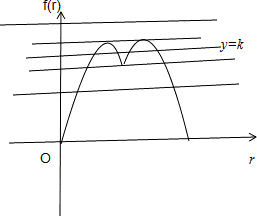
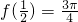 .关于r的方程f(r)=k的解的个数可能为0,2,3,4.
.关于r的方程f(r)=k的解的个数可能为0,2,3,4.

 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P在平面DD1C1C内,PD1=PC1=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com