练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝x2－2ax＋5在(－∞，2]上是减函数，且对任意的x1，x2∈[1，a＋1]，总有|f(x1)－f(x2)|≤4，则实数a的取值范围为______．

     

    [2,3]

    【解析】函数f(x)＝(x－a)2＋5－a2在(－∞，2]上是减函数，∴a≥2，函数f(x)在[1，a]上是减函数，在[a，a＋1]上是增函数，要使x1，x2∈[1，a＋1]时，总有|f(x1)－f(x2)|≤4，

    只要

    又f(1)≥f(a＋1)，∴只要f(1)－f(a)≤4，即(6－2a)－(5－a2)≤4，解得－1≤a≤3.又a≥2，故2≤a≤3.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：选择题

    某工厂需要建一个面积为512 m2的矩形堆料场，一边可以利用原有的墙壁，其他三边需要砌新的墙壁，当砌新墙所用材料最省时，堆料场的长和宽的比为(　　)

    A．1 B．2 C.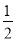 D.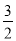

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：解答题

    已知lgx＋lgy＝2 lg(2x－3y)，求的值．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    已知2a＝5b＝，则＋＝(　　)

    A. B．1 C. D．2

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：填空题

    对任意实数a，b，函数F(a，b)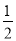＝(a＋b－|a－b|)，如果函数f(x)＝－x2＋2x＋3，g(x)＝x＋1，那么函数G(x)＝F(f(x)，g(x))的最大值等于________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题

    若函数f(x)＝x2－ax－a在区间[0,2]上的最大值为1，则实数a等于(　　)

    A．－1 B．1 C．2 D．－2

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：选择题

    若函数f(x)、g(x)分别是R上的奇函数、偶函数，且满足f(x)－g(x)＝ex，则有(　　)

    A．f(2)<f(3)<g(0) B．g(0)<f(3)<f(2)

    C．f(2)<g(0)<f(3) D．g(0)<f(2)<f(3)

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：解答题

    已知函数f(x)＝a－.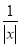

    (1)求证：函数y＝f(x)在(0，＋∞)上是增函数；

    (2)若f(x)<2x在(1，＋∞)上恒成立，求实数a的取值范围．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-11导数的应用一（解析版） 题型：解答题

    已知函数f(x)＝xlnx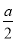－x2.

    (1)当a＝1时，函数y＝f(x)有几个极值点？

    (2)是否存在实数a，使函数f(x)＝xlnx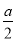－x2有两个极值？若存在，求实数a的取值范围；若不存在，请说明理由．

     

    查看答案和解析>>

    同步练习册答案