
如图,△ABC是等边三角形,PA⊥平面ABC,DC∥PA,且DC=AC=2PA=2,E是BD的中点.
(Ⅰ)求证:AE⊥BC;
(Ⅱ)求点D到平面PBC的距离.
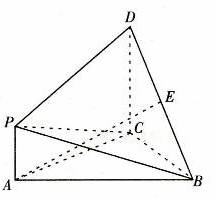
(Ⅰ)证明:取BC的中点F,连接EF,AF,则EF∥DC,
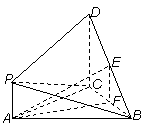 ∵DC⊥平面ABC,∴DC⊥BC,则EF⊥BC;
∵DC⊥平面ABC,∴DC⊥BC,则EF⊥BC;
由△ABC是等边三角形知,AF⊥BC,
∴BC⊥平面AEF,
∵AE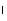 平面AEF,∴AE⊥BC.
平面AEF,∴AE⊥BC.
(Ⅱ)取AC的中点H,连接BH,
∴BH⊥AC,又∵平面PACD⊥平面ABC,
∴BH⊥平面PACD,且BH=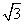 ;
;
又PA⊥平面ABC,PA∥DC,DC⊥平面ABC,则,PA⊥AC,
由AB=AC=DC=2PA=2知,S△PCD=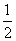 DC·AC=2,
DC·AC=2,
∴VB-PCD=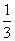 S△PCD·BE=
S△PCD·BE=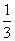 ×2×
×2×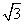 =
=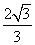
在Rt△PAF中,可求PF=2,S△PBC=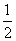 BC·PF=2;
BC·PF=2;
设点D到平面PBC的距离为h,由VD-PBC=VB-PCD得:
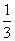 S△PBC·h=
S△PBC·h=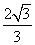 ,∴h=
,∴h=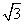 ,
,
即点D到平面PBC的距离为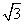 .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
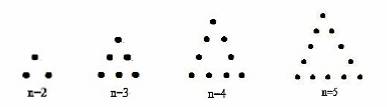
如图所示,将若干个点摆成三角形图案,每条边(包括两个端点)有n(n>1,n∈N*)个点,相应的图案中总的点数记为an,按上述规律,则a6= _________ ,an= _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,∠C=90°,BC=2,AC=4,AB边上点P到边AC、BC的距离乘积的取值范围是( )
|
| A. | [0,2] | B. | [0,3] | C. | [0,4] | D. | [0, |
查看答案和解析>>
科目:高中数学 来源: 题型:
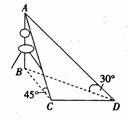
如图,要测量底部不能到达的某铁塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°.在水平面上测得∠BCD=120°,C、D两地相距600m,则铁塔AB的高度是( )
|
| A. | 120 | B. | 480m | C. | 240 | D. | 600m |
查看答案和解析>>
科目:高中数学 来源: 题型:
某人忘记了自己的文档密码,但记得该密码是由一个2,一个9,两个6组成的四位数,
于是用这四个数随意排成一个四位数,输入电脑尝试,那么他找到自己的文档密码最多
尝试次数为
A.36 B.24 C.18 D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com