
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{1+\sqrt{5}}}{2}$ | D. | $\frac{{-1+\sqrt{5}}}{2}$ |
分析 由题意写出菱形ABCD一边AD所在直线方程,由坐标原点O到AD的距离等于c列式求得关于e的方程,求解方程得答案.
解答 解:菱形ABCD一边AD所在直线方程为$\frac{x}{a}+\frac{y}{b}=1$,即bx+ay-ab=0,
由题意,坐标原点O到AD的距离d=$\frac{|-ab|}{\sqrt{{a}^{2}+{b}^{2}}}=c$,
整理可得 c4-3a2c2+a4=0,即:e4-3e2+1=0,
解得:$e=\frac{{-1±\sqrt{5}}}{2},e=\frac{{-1+\sqrt{5}}}{2}$,$e=\frac{{-1-\sqrt{5}}}{2}$(舍去),
∴椭圆的离心率e=$\frac{{-1+\sqrt{5}}}{2}$.
故选:D.
点评 本题考查椭圆的简单性质,考查了直线与圆位置关系的应用,训练了点到直线距离公式的应用,是中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | $\frac{{4\sqrt{5}}}{5}$ | D. | $\frac{{8\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
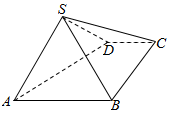 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形,AB=BC=2,CD=1,SD=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l | B. | 2 | C. | 4 | D. | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com