练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

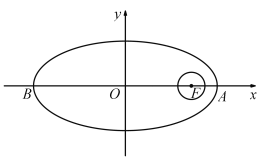
    【题目】我国计划发射火星探测器，该探测器的运行轨道是以火星（其半径）的中心为一个焦点的椭圆．如图，已知探测器的近火星点（轨道上离火星表面最近的点）到火星表面的距离为，远火星点（轨道上离火星表面最远的点）到火星表面的距离为．假定探测器由近火星点第一次逆时针运行到与轨道中心的距离为时进行变轨，其中分别为椭圆的长半轴、短半轴的长，求此时探测器与火星表面的距离（精确到）．

    【答案】

    【解析】

    根据题意求出轨道方程为，设变轨时，探测器位于，则，结合轨道方程求出，再利用两点间的距离公式即可求解.

    设所求轨道方程为

    ．．

    于是．所以所求轨道方程为．

    设变轨时，探测器位于，则

    ．

    解方程组，得（由题意）．

    所以探测器在变轨时与火星表面的距离为．

    所以探测器在变轨时与火星表面的距离约为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图1，一艺术拱门由两部分组成，下部为矩形，的长分别为和，上部是圆心为的劣弧，．

    （1）求图1中拱门最高点到地面的距离；

    （2）现欲以B点为支点将拱门放倒，放倒过程中矩形所在的平面始终与地面垂直，如图2、图3、图4所示．设与地面水平线所成的角为．记拱门上的点到地面的最大距离为，试用的函数表示，并求出的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    （I）求函数的极值；

    （II）若方程仅有一个实数解，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】

    已知双曲线设过点的直线l的方向向量

    （1） 当直线l与双曲线C的一条渐近线m平行时，求直线l的方程及l与m的距离；

    （2） 证明：当>时，在双曲线C的右支上不存在点Q，使之到直线l的距离为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆，直线.

    （1）证明：不论取什么数，直线与圆恒交于两点；

    （2）求直线被圆截得的线段的最短长度，并求此时的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

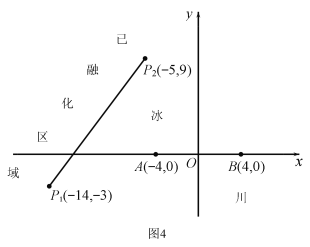
    【题目】为了考察冰川的融化状况，一支科考队在某冰川山上相距8km的A、B两点各建一个考察基地，视冰川面为平面形，以过A、B两点的直线为x轴，线段AB的垂直平分线为y轴建立平面直角坐标系（图4）．考察范围到A、B两点的距离之和不超过10km的区域．

    （I）求考察区域边界曲线的方程：

    （II）如图4所示，设线段是冰川的部分边界线（不考虑其他边界），当冰川融化时，边界线沿与其垂直的方向朝考察区域平行移动，第一年移动0.2km，以后每年移动的距离为前一年的2倍．问：经过多长时间，点A恰好在冰川边界线上？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三个圆交于一点，又两两将于点、、.以为圆心的一个圆与上述三个圆分别交于点，，，其中，点在不含点的圆上，等等.又设、、的外接圆交于一点， 、的外接圆交于一点.证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】p：关于x的方程无解，q：（）

    （1）若时，“”为真命题，“”为假命题，求实数a的取值范围．

    （2）当命题“若p，则q”为真命题，“若q，则p”为假命题时，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列中，．

    （1）求数列的通项；

    （2）满足的共有几项？

    查看答案和解析>>

    同步练习册答案