
 ij����Ʒר����ľ�Ӫ������ʾ���£�
ij����Ʒר����ľ�Ӫ������ʾ���£����� ��1�����ô�����ϵ����������������Ľ���ʽ���ٸ���������Q���ټ��������ۼ۸�P��Ԫ������ĺ�����ϵʽ������������Q���ټ��������ۼ۸�P��Ԫ���ĺ�����ϵ��
��2����õ�������ΪLԪ�����������L=Q��P-14����100-100���õ������Ľ���ʽ���ֶ������������ֵ���Ƚϼ��ɣ�
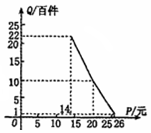
��� �⣺��1���ߵ㣨14��22������20��10������26��1���ں�����ͼ���ϣ�
��$\left\{\begin{array}{l}{14{k}_{1}+{b}_{1}=22}\\{20{k}_{1}+{b}_{1}=10}\end{array}\right.$�����$\left\{\begin{array}{l}{{k}_{1}=-2}\\{{b}_{1}=50}\end{array}\right.$��
ͬ���ɵ�$\left\{\begin{array}{l}{{k}_{2}=-\frac{3}{2}}\\{{b}_{2}=40}\end{array}\right.$��
��Q=$\left\{\begin{array}{l}{-2P+50��14��P��20}\\{-\frac{3}{2}P+40��20��P��26}\end{array}\right.$��
��2����õ�������ΪLԪ�����������L=Q��P-14����100-100��
�ɣ�1����L=$\left\{\begin{array}{l}{��-2p+50����P-14����100-4400��14��P��20}\\{��-\frac{3}{2}P+40����P-14����100-4400��20��P��26}\end{array}\right.$��
=$\left\{\begin{array}{l}{-200{P}^{2}+7800P-74400��14��P��20}\\{-150{P}^{2}+6100P-10000��20��P��26}\end{array}\right.$��
��14��p��20ʱ��Lmax=1650Ԫ����ʱP=$\frac{39}{2}$Ԫ��
��20��p��26ʱ��Lmax=$\frac{4850}{3}$Ԫ����ʱP=$\frac{61}{3}$Ԫ��
�ʵ�P=$\frac{39}{2}$ʱ�����������Ϊ1650Ԫ��
���� ������Ҫ�����뺯����Ӧ�����⣬������������������ϵ�����ö��κ�����ͼ��������Ǽ��ɵõ����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �溯�� | B�� | ż���� | C�� | �溯����ż���� | D�� | �����ż���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��-1 | B�� | -1 | C�� | 1 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�1�� | B�� | ��1��+�ޣ� | C�� | ��-�ޣ�3�� | D�� | ��3��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 60�� | C�� | 90�� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com