
分析 (1)利用平面向量的坐标运算,求出|$\overrightarrow{AB}$|,|$\overrightarrow{AC}$|,$\overrightarrow{AB}$•$\overrightarrow{AC}$,根据夹角公式求解.
(2)利用向量的平行关系,求出m的值,在求解|$\overrightarrow{OD}$|.
解答 解:(1)由题意:A(3,1),B(1,0),C(2,3),
∴$\overrightarrow{AB}=({-2,-1}),\overrightarrow{AC}=({-1,2})$,∴$|\overrightarrow{AB}|=|\overrightarrow{AC}|=\sqrt{5}$,
∵$\overrightarrow{AB}•\overrightarrow{AC}=2-2=0$,故AB⊥AC,
因此△ABC是等腰直角三角形.
(2)∵O为坐标原点,$\overrightarrow{OD}$=m$\overrightarrow{OC}$(m∈R),$\overrightarrow{OC}$=(2,3),$\overrightarrow{BC}$=(1,3)
由$(\overrightarrow{AB}-m\overrightarrow{OC})$∥$\overrightarrow{BC}$得:(-2-2m,-1-3m)∥(1,3),⇒-6-6m=-1-3m
解得:$m=-\frac{5}{3}$,
所以$|\overrightarrow{OD}|=|m|•|\overrightarrow{OC}|=\frac{{5\sqrt{13}}}{3}$.
点评 本题考查了平面向量的基本运算,考查了向量垂直与数量积的关系,属于中档题.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:解答题
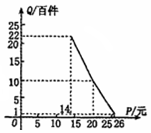 某消费品专卖店的经营资料显示如下:
某消费品专卖店的经营资料显示如下:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-1,\frac{3}{2}})$ | B. | $({-∞,-1})∪({\frac{3}{2},+∞})$ | C. | $({1,\frac{3}{2}})$ | D. | $({-∞,1})∪({\frac{3}{2},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
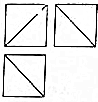 一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,已知三视图中每个正方形边长为1,则此三视图所对应几何体的体积为( )
一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,已知三视图中每个正方形边长为1,则此三视图所对应几何体的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2016}{{2}^{2016}}$ | B. | 2016×22015 | C. | 2016×22016 | D. | $\frac{2016}{{2}^{2015}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com