
【题目】已知函数![]() 为定义域
为定义域![]() 上的奇函数,且在
上的奇函数,且在![]() 上是单调递增函数,函数
上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,
为等差数列,![]() ,且公差不为0,若
,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45 B. 15 C. 10 D. 0
【答案】A
【解析】
根据题意,由奇函数的性质可得(-x)+f(x)=0,又由g(x)=f(x-5)+x且g(a1)+g(a2)+…+g(a9)=45,可得f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,结合等差数列的性质可得f(a1-5)=-f(a9-5)=f(5-a9),进而可得a1-5=5-a9,即a1+a9=10,进而计算可得答案.
根据题意,函数y=f(x)为定义域R上的奇函数,
则有f(-x)+f(x)=0,
∵g(x)=f(x-5)+x,
∴若g(a1)+g(a2)+…+g(a9)=45,
即f(a1-5)+a1+f(a2-5)+a2+…+f(a9-5)+a9=45,
即f(a1-5)+f(a2-5)+…+f(a9-5)+(a1+a2+…+a9)=45,
f(a1-5)+f(a2-5)+…+f(a9-5)=0,
又由y=f(x)为定义域R上的奇函数,且在R上是单调函数,
f(a1-5)+f(a2-5)+…+f(a9-5)是9项的和且和为0,
必有f(a1-5)+f(a9-5)=0,
则有a1-5=5-a9,
即a1+a9=10,
在等差数列中,a1+a9=10=2a5,
即a5=5,
则a1+a2+…+a9=9a5=45;
故选:A.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
【题目】等腰△ABC中,AC=BC= ![]() ,AB=2,E,F分别为AC,BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP=
,AB=2,E,F分别为AC,BC的中点,将△EFC沿EF折起,使得C到P,得到四棱锥P﹣ABFE,且AP=BP= ![]() .
. 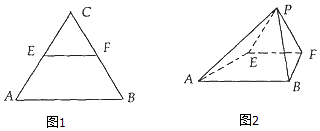
(1)求证:平面EFP⊥平面ABFE;
(2)求二面角B﹣AP﹣E的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机调查了50人,他们年龄的频数分布及支持“生育二胎”人数如表:
年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
(1)由以上统计数据填下面2乘2列联表,并问是否有的99%把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异:
(2)若对年龄在[5,15),[35,45)的被调查人中各随机选取两人进行调查,记选中的4人不支持“生育二胎”人数为ξ,求随机变量ξ的分布列及数学期望;
年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
支持 | a= | c= | |
不支持 | b= | d= | |
合计 |
参考数据:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过原点的动直线l与圆![]() 相交于不同的两点A,B.
相交于不同的两点A,B.
(1)求线段AB的中点M的轨迹C的方程;
(2)是否存在实数k,使得直线L:y=k(x﹣4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,BC= ![]() ,AB=AC=AA1=1,D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1 .
,AB=AC=AA1=1,D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1 . 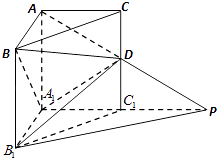
(1)求证:CD=C1D;
(2)求二面角A1﹣B1D﹣P的平面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com