
分析 ( I)利用两个向量垂直的性质,两个向量数量积的运算,求得tanα和sinα的值.
( II)利用同角三角函数的基本关系、两角和的正弦公式,求得sinβ的值.
解答 解:(Ⅰ)∵$\vec a⊥\vec b$且$\vec a=(cosα,3)$,$\vec b=(-4,sinα)$,∴-4cosα+3sinα=0,
即3sinα=4cosα,∴$tanα=\frac{4}{3}$.
联立 $\left\{\begin{array}{l}3sinα=4cosα\\{sin^2}α+{cos^2}α=1\end{array}\right.$,解得$sinα=±\frac{4}{5}$,
又$0<α<\frac{π}{2}$,∴$sinα=\frac{4}{5}$.
(Ⅱ)由(Ⅰ)易求得$cosα=\frac{3}{5}$,
又$0<α<\frac{π}{2}<β<π$,∴$-\frac{π}{2}<-α<0,\frac{π}{2}<β<π$,∴0<β-α<π,
∴$sin(β-α)=\sqrt{1-{{cos}^2}(β-α)}=\sqrt{1-{{(\frac{{\sqrt{2}}}{10})}^2}}=\frac{{7\sqrt{2}}}{10}$,
∴sinβ=sin[(β-α)+α]=sin(β-α)cosα+cos(β-α)sinα=$\frac{{7\sqrt{2}}}{10}•\frac{3}{5}+\frac{{\sqrt{2}}}{10}•\frac{4}{5}=\frac{{\sqrt{2}}}{2}$.
点评 本题主要考查两个向量垂直的性质,两个向量数量积的运算,同角三角函数的基本关系、两角和的正弦公式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{15}{11}$ | C. | -1 | D. | $\frac{17}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | B⊆∁RA | B. | A⊆∁RB | C. | B⊆A | D. | A⊆B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,-1) | B. | [-3,-1] | C. | (-∞,-3]∪[-1,+∞) | D. | (-∞,-3)∪(-1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
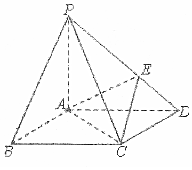 在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.
在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E在PD上,且PE:ED=2:1,面PAB∩面PCD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2016) | B. | (-∞,-2018) | C. | (-2018,0) | D. | (-2016,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<0} | B. | {x|0<x≤1} | C. | {x|0≤x≤2} | D. | {x|0≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$ | B. | -$\frac{3}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com