Question

【题目】已知函数f（x）=|x+2|﹣2|x﹣1|．
（1）解不等式f（x）≥﹣2；
（2）对任意x∈R，都有f（x）≤x﹣a成立，求实数a的取值范围．

Answer 1

【答案】
（1）解：f（x）= ．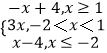

∵f（x）≥﹣2，

∴ 或 或 ，

解得1≤x≤6或﹣ ≤x＜1．

∴不等式f（x）≥﹣2的解为集为{x|﹣ ≤x≤6}．

（2）解：当x≥1时，﹣x+4≤x﹣a，即a≤2x﹣4恒成立，∴a≤﹣2；

当﹣2＜x＜1时，3x≤x﹣a，即a≤﹣2x恒成立，∴a≤﹣2；

当x≤﹣2时，x﹣4≤x﹣a，即a≤4恒成立．

∵任意x∈R，都有f（x）≤x﹣a成立，

∴a≤﹣2

【解析】（1）去绝对值符号得出f（x）的分段解析式，再各段上解不等式即可；（2）对x的范围进行讨论，分离参数得出a在各段上的最小值，即可得出a的范围．
【考点精析】解答此题的关键在于理解不等式的证明的相关知识，掌握不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．