
【题目】设函数![]()
(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若![]() ,求证:在
,求证:在![]() 时,
时, ![]() .
.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)先求出![]() ,通过
,通过![]() 在点
在点![]() 处的切线斜率,可得
处的切线斜率,可得![]() ,解得
,解得![]() ;(2)由(1)知:
;(2)由(1)知: ![]() ,结合导数分①
,结合导数分①![]() 、②
、②![]() 两种情况讨论分别令
两种情况讨论分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;;(3)通过变形,只需证明
的减区间;;(3)通过变形,只需证明![]() 即可,利用
即可,利用![]() ,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
,根据指数函数及幂函数的性质、函数的单调性及零点判定定理即得到结论.
试题解析:(1)若![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,
,
![]() ,
,
得![]() .
.
(2)由![]()
当![]() 时,令
时,令![]() 解得:
解得: ![]()
当![]() 变化时,
变化时, ![]() 随
随![]() 变化情况如表:
变化情况如表:
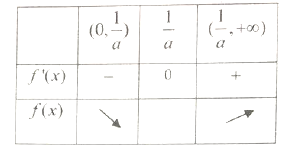
由表可知: ![]() 在
在![]() 上是单调减函数,在
上是单调减函数,在![]() 上是单调增函数
上是单调增函数
当![]() 时,
时, ![]() ,
, ![]() 的单调减区间为
的单调减区间为![]()
所以,当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]() .单调增区间为
.单调增区间为![]()
当![]() 时,
时, ![]() 的单调减区间为
的单调减区间为![]()
(3)当![]() 时,要证
时,要证![]() ,即证
,即证![]()
令![]() ,只需证
,只需证![]()
∵![]()
由指数函数及幕函数的性质知: ![]() 在
在![]() 上是增函数
上是增函数
∵![]() ,∴
,∴![]() 在
在![]() 内存在唯一的零点,
内存在唯一的零点,
也即![]() 在
在![]() 上有唯一零点
上有唯一零点
设![]() 的零点为
的零点为![]() ,则
,则![]() ,即
,即![]() ,
,
由![]() 的单调性知:
的单调性知:
当![]() 时,
时, ![]() ,
, ![]() 为减函数
为减函数
当![]() 时,
时, ![]() ,
, ![]() 为增函数,
为增函数,
所以当![]() 时.
时.
![]()
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+2|﹣2|x﹣1|.
(1)解不等式f(x)≥﹣2;
(2)对任意x∈R,都有f(x)≤x﹣a成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinx+1. (Ⅰ)设ω为大于0的常数,若f(ωx)在区间 ![]() 上单调递增,求实数ω的取值范围;
上单调递增,求实数ω的取值范围;
(Ⅱ)设集合 ![]() ,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
,B={x||f(x)﹣m|<2},若A∪B=B,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c且b=c,∠A的平分线为AD,若 ![]() =m
=m ![]()
![]() .
.
(1)当m=2时,求cosA
(2)当 ![]() ∈(1,
∈(1, ![]() )时,求实数m的取值范围.
)时,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项为正的数列{an}是等比数列,a1=2,a5=32,数列{bn}满足:对于任意n∈N* , 有a1b1+a2b2+…+anbn=(n﹣1)2n+1+2.
(1)求数列{an}的通项公式;
(2)令f(n)=a2+a4+…+a2n , 求 ![]() 的值;
的值;
(3)求数列{bn}通项公式,若在数列{an}的任意相邻两项ak与ak+1之间插入bk(k∈N*)后,得到一个新的数列{cn},求数列{cn}的前100项之和T100 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意的实数满足:f(x+3)=﹣ ![]() ,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2016)= .
,且当﹣3≤x<﹣1时,f(x)=﹣(x+2)2 , 当﹣1≤x<3时,f(x)=x.则f(1)+f(2)+f(3)+…+f(2016)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,满足:a2+c2=b2+ ![]() ac
ac
(1)求∠B 的大小;
(2)求 ![]() cosA+cosC 的最大值.
cosA+cosC 的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com