
| A. | $\frac{\sqrt{17}}{9}$ | B. | $\frac{-2\sqrt{2}}{3}$ | C. | -$\frac{\sqrt{17}}{9}$ | D. | $\frac{\sqrt{17}}{9}$或-$\frac{\sqrt{17}}{9}$ |
分析 把已知等式两边平方,可得2sinαcosα<0,得到α∈($\frac{π}{2},π$),则sinα>0,cosα<0,进一步求得sinα-cosα,与原等式联立求出sinα,代入二倍角余弦求解.
解答 解:由sin α+cos α=$\frac{1}{3}$,两边平方得$si{n}^{2}α+co{s}^{2}α+2sinαcosα=\frac{1}{9}$,
∴$2sinαcosα=-\frac{8}{9}$,
又α∈(0,π),∴α∈($\frac{π}{2},π$),
则sinα>0,cosα<0,
∴sinα-cosα=$\sqrt{(sinα-cosα)^{2}}=\sqrt{1-2sinαcosα}$=$\sqrt{1+\frac{8}{9}}=\frac{\sqrt{17}}{3}$.
联立$\left\{\begin{array}{l}{sinα+cosα=\frac{1}{3}}\\{sinα-cosα=\frac{\sqrt{17}}{3}}\end{array}\right.$,得sinα=$\frac{\sqrt{17}+1}{6}$.
∴cos2α=1-2sin2α=1-2×$(\frac{\sqrt{17}+1}{6})^{2}$=$-\frac{\sqrt{17}}{9}$.
故选:C.
点评 本题考查二倍角的余弦,关键是由已知可得α∈($\frac{π}{2},π$),是中档题.


科目:高中数学 来源: 题型:选择题
| A. | x2-$\frac{{y}^{2}}{4}$=1 | B. | x2-$\frac{{y}^{2}}{3}$=1 | C. | x2-y2=1 | D. | x2-$\frac{{y}^{2}}{2}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都能被5整除 | B. | a,b都不能被5整除 | ||
| C. | a,b有一个能被5整除 | D. | a,b有一个不能被5整除 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
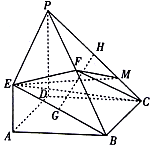 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com