
【题目】已知函数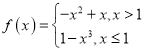 ,若函数
,若函数![]() 恰有三个零点,则实数
恰有三个零点,则实数![]() 的取值范围是____________.
的取值范围是____________.
【答案】![]()
【解析】
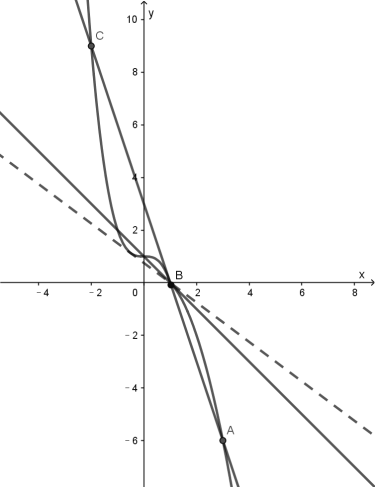
画出![]() 和
和![]() 的图像,根据
的图像,根据![]() 和
和![]() 的图像有三个交点,求得
的图像有三个交点,求得![]() 的取值范围.
的取值范围.
注意到![]() 在
在![]() 上递减,且关于
上递减,且关于![]() 对称.画出
对称.画出![]() 和
和![]() 的图像如下图所示,直线
的图像如下图所示,直线![]() 过定点
过定点![]() .由于
.由于![]() ,所以
,所以![]() 是
是![]() 的零点.
的零点.
由图像可知,当![]() 时,
时,![]() 与
与![]() 只有一个公共点
只有一个公共点![]() .
.
当![]() 时:
时:
由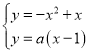 化简得
化简得![]() ,由于
,由于![]() 时,
时,![]() ,所以当
,所以当![]() 时,
时,![]() ,不在区间
,不在区间![]() 内,所以此时
内,所以此时![]() 与
与![]() 没有公共点.当
没有公共点.当![]() 时,
时,![]() ,在区间
,在区间![]() 内,所以此时
内,所以此时![]() 与
与![]() 有一个公共点.
有一个公共点.
当![]() ,且
,且![]() 时,由图可知,要使
时,由图可知,要使![]() 与
与![]() 有
有![]() 个公共点,
个公共点,![]() 的取值范围应介于
的取值范围应介于![]() 和过
和过![]() 点的
点的![]() 切线(虚线)的斜率之间.设切点为
切线(虚线)的斜率之间.设切点为![]() ,
,![]() ,所以
,所以![]() ,解得
,解得![]() ,切线的斜率为
,切线的斜率为![]() .所以当
.所以当![]() 时,符合题意.
时,符合题意.
当![]() ,且
,且![]() 时,由图可知,要使
时,由图可知,要使![]() 与
与![]() 有
有![]() 个公共点,
个公共点,![]() 的取值范围应不大于过
的取值范围应不大于过![]() 点
点![]() 的切线的斜率.
的切线的斜率.![]() ,
,![]() .所以当
.所以当![]() 时符合题意.
时符合题意.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
故答案为:![]() .
.


科目:高中数学 来源: 题型:
【题目】某省从2021年开始将全面推行新高考制度,新高考“![]() ”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为
”中的“2”要求考生从政治、化学、生物、地理四门中选两科,按照等级赋分计入高考成绩,等级赋分规则如下:从2021年夏季高考开始,高考政治、化学、生物、地理四门等级考试科目的考生原始成绩从高到低划分为![]() 五个等级,确定各等级人数所占比例分别为
五个等级,确定各等级人数所占比例分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等级考试科目成绩计入考生总成绩时,将
,等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法分别转换到
等级内的考生原始成绩,依照等比例转换法分别转换到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
五个分数区间,得到考生的等级分,等级转换分满分为100分.具体转换分数区间如下表:
等级 |
|
|
|
|
|
比例 |
|
|
|
|
|
赋分区间 |
|
|
|
|
|
而等比例转换法是通过公式计算:![]()
其中![]() ,
,![]() 分别表示原始分区间的最低分和最高分,
分别表示原始分区间的最低分和最高分,![]() 、
、![]() 分别表示等级分区间的最低分和最高分,
分别表示等级分区间的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示转换分,当原始分为
表示转换分,当原始分为![]() ,
,![]() 时,等级分分别为
时,等级分分别为![]() 、
、![]()
假设小南的化学考试成绩信息如下表:
考生科目 | 考试成绩 | 成绩等级 | 原始分区间 | 等级分区间 |
化学 | 75分 |
|
|
|
设小南转换后的等级成绩为![]() ,根据公式得:
,根据公式得:![]() ,
,
所以![]() (四舍五入取整),小南最终化学成绩为77分.
(四舍五入取整),小南最终化学成绩为77分.
已知某年级学生有100人选了化学,以半期考试成绩为原始成绩转换本年级的化学等级成绩,其中化学成绩获得![]() 等级的学生原始成绩统计如下表:
等级的学生原始成绩统计如下表:
成绩 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人数 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)从化学成绩获得![]() 等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
等级的学生中任取2名,求恰好有1名同学的等级成绩不小于96分的概率;
(2)从化学成绩获得![]() 等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为
等级的学生中任取5名,设5名学生中等级成绩不小于96分人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年10月,德国爆发出“芳香烃门”事件,即一家权威的检测机构在德国销售的奶粉中随机抽检了16款(德国4款,法国8款、荷兰4款),其中8款检测出芳香烃矿物油成分,此成分会严重危害婴幼儿的成长,有些奶粉已经远销至中国,![]() 地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香矿物油成分,则随机抽取3袋恰有2袋含有芳香经矿物油成分的概率为( )
地区闻讯后,立即组织相关检测员对这8款品牌的奶粉进行抽检,已知该地区一婴幼儿用品商店在售某品牌的奶粉共6袋,这6袋奶粉中有4袋含有芳香矿物油成分,则随机抽取3袋恰有2袋含有芳香经矿物油成分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,如图所示,在宝塔形数表中位于第![]() 行,第
行,第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ( )
( )
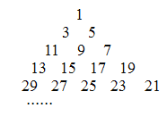
A.64B.65C.71D.72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为4,直线
的长轴长为4,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 的右顶点作互相垂直的两条直线
的右顶点作互相垂直的两条直线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点(点
两点(点![]() 不同于椭圆
不同于椭圆![]() 的右顶点),证明:直线
的右顶点),证明:直线![]() 过定点
过定点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
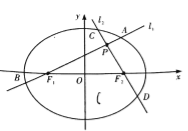
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且此抛物线的准线被椭圆C截得的弦长为1.
的焦点重合,且此抛物线的准线被椭圆C截得的弦长为1.
(I)求椭圆C的标准方程;
(II)直线l交椭圆C于A,B两点,线段AB的中点为![]() ,直线m是线段AB的垂直平分线,试问直线
,直线m是线段AB的垂直平分线,试问直线![]() 过定点坐标.
过定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
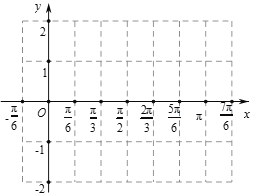
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com