Question

【题目】已知函数f（x）=|x|+ ﹣1（x≠0）
（1）当m=1时，判断f（x）在（﹣∞，0）的单调性，并用定义证明；
（2）若对任意x∈（1，+∞），不等式 f（log2x）＞0恒成立，求m的取值范围．
（3）讨论f（x）零点的个数．

Answer 1

【答案】
（1）

解：由当m=1，且x＜0时，f（x）=﹣x+ ﹣1是单调递减的．

证明：设x1＜x2＜0，则

f（x1）﹣f（x2）=﹣x1+ ﹣1﹣（﹣x2+ ﹣1）=x2﹣x1+ ﹣

=（x2﹣x1）﹣ =（x2﹣x1）（1+ ），

∵x1＜x2＜0，则x2﹣x1＞0，x1x2＞0，则有f（x1）﹣f（x2）＞0，

f（x1）＞f（x2）

则f（x）在（﹣∞，0）上为减函数

（2）

解：由 f（log2x）＞0得|log2x|+ ﹣1＞0，

当x∈（1，+∞），log2x＞0，

则不等式变形为（log2x）2﹣log2x+m＞0，

即m＞﹣（log2x）2+log2x，

而g（x）=﹣（log2x）2+log2x=﹣（log2x﹣ ）2+ ，

当log2x= ，即x= 时，g（x）取得最大值 ，

∴m＞ ．

（3）

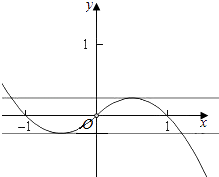
解：由f（x）=0可得x|x|﹣x+m=0，变为m=﹣x|x|+x，x≠0

令h（x）=x﹣x|x|=

作出函数h（x）的图象及直线y=m，由图象可得：

当m＞ 或m＜﹣ 时，f（x）有1个零点．

当m= 或m=0或m=﹣ 时，f（x）有2个零点；

当0＜m＜ 或﹣ ＜m＜0时，f（x）有3个零点．

【解析】（1）f（x）在（﹣∞，0）上为减函数．运用函数的单调性的定义加以证明，注意取值、作差、变形和定符号、下结论几个步骤；（2）利用不等式恒成立，进行转化求解即可，（3）利用函数与方程的关系进行转化，利用参数分离法结合数形结合进行讨论即可．
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点，需要掌握单调性的判定法：①设x1,x2是所研究区间内任两个自变量，且x1＜x2；②判定f(x1)与f(x2)的大小；③作差比较或作商比较才能正确解答此题．