
分析 求出各复数的模和辐角可将复数的代数形式化为三角形式
解答 解:(1)z=3$\sqrt{3}$+3i=6($\frac{\sqrt{3}}{2}$+$\frac{1}{2}$i)=6(cos$\frac{π}{6}$+isin$\frac{π}{6}$);
(2)z=4-4i=4$\sqrt{2}$($\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{2}$i)=4$\sqrt{2}$(cos$\frac{7π}{4}$+isin$\frac{7π}{4}$);
(3)z=-6i=6(cos$\frac{3π}{2}$+isin$\frac{3π}{2}$).
点评 本题考查了复数代数形式与三角形式的转化问题,计算出各复数的模和辐角,是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
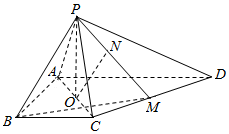 如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.
如图,四棱锥P-ABCD,AD∥BC,AD=2BC=4,AB=2$\sqrt{3}$,∠BAD=90°,M,O分别为CD和AC的中点,PO⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+48y-3=0 | B. | x+80y-5=0 | C. | x+3y-3=0 | D. | x+5y-5=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com