
| x |
| lnx |
| e |
| lnx-1 |
| (lnx)2 |
| e |
| e |
| lnx-1 |
| (lnx)2 |
| 1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| e |
| e |
| e |
| 1 |
| 2 |
| 1 |
| lnx |
| 1 |
| 2 |
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| e |
| 1 |
| 4 |
| 1 |
| 4 |
| e |
| e2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4e2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4e2 |
| 1 |
| 2 |
| 1 |
| 4 |
| e |
| 1 |
| 2 |
| lnx-1 |
| (lnx)2 |
| e |
| e |
| x0 |
| lnx0 |
| 1 |
| 4 |
| 1 |
| 4x0 |
| 1 |
| lnx0 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4e2 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
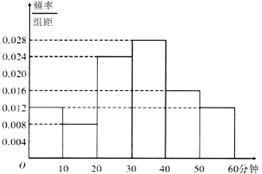 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.| 非汉语关注者 | 汉语关注者 | 合 计 | |
| 教育工作者 | 6 | ||
| 非教育工作者 | 30 | ||
| 合 计 | 22 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
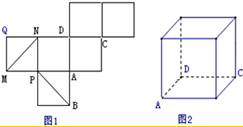 图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com