练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在锐角三角形ABC中,已知内角A、B、C所对的边分别为a、b、c,且(tanA-tanB)=1+tanA·tanB.

    (1)若a2-ab=c2-b2,求A、B、C的大小;

    (2)已知向量m=(sinA,cosA),n=(cosB,sinB),求|3m-2n|的取值范围.

    (理)解:∵(tanA-tanB)=1+tanA·tanB,4

    又△ABC为锐角三角形,

    ∴=.

    ∴tan(A-B)=.

    ∵0＜A＜,0＜B＜,

    ∴-＜A-B＜.

    ∴A-B=.

    (1)∵a2-ab=c2-b2,

    ∴cosC==.

    ∴C=.

    由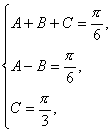

    解得A=,B=.

    ∴A=,B=,C=.

    (2)|3m-2n|2=9m2+4n2-12m·n

    =13-12(sinAcosB+cosAsinB)

    =13-12sin(A+B)

    =13-12sin(2B+).

    ∵△ABC为锐角三角形,A-B=,

    ∴C=π-A-B＜,A=+B＜.

    ∴＜B＜,＜2B+＜.

    ∴sin(2B+)∈(,1).

    ∴|3m-2n|2∈(1,7).

    ∴|3m-2n|的取值范围是(1,).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在锐角三角形ABC中，a，b，c分别是角A，B，C的对边，且a=2bsinA．
    （1）求∠B的大小；
    （2）若a=3
    		3
    ，c=5    ，求边b的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在锐角三角形ABC中，a，b，c分别为内角A，B，C所对的边，且满足
    		3
    a-2bsinA=0    ．
    （Ⅰ）求角B的大小；
    （Ⅱ）若b=
    		7
    ，c=2，求
    AB
    •
    AC
    的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在锐角三角形ABC中，a，b，c分别是角A、B、C的对边，
    p
    =(a+c，b)，
    q
    =（c-a，b-c）且
    p
    ⊥
    q

    （1）求A的大小；
    （2）记f(B)=2sin2B+sin(2B+
    π
    6
    )    ，求f（B）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•南充一模）在锐角三角形ABC中，角A，B，C对边a，b，c且a2+b2-
    		2
    ab=c2，tanA-tanB=csc2A
    ①求证：2A-B=
    π
    2
    ；
    ②求三角形ABC三个角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知命题p：在锐角三角形ABC中，?A，B，使sinA＜cosB；命题q：?x∈R，都有x2+x+1＞0，给出下列结论：
    ①命题“p∧q”是真命题；           
    ②命题“￢p∨q”是真命题；
    ③命题“￢p∨￢q”是假命题；       
    ④命题“p∧￢q”是假命题；
    其中正确结论的序号是（　　）

    查看答案和解析>>

    同步练习册答案