
分析 由已知得所截矩形样式只有一种,其各边分别与正方开形平行,设矩形一边MN为x($\frac{5a}{6}≤x≤a$),得到矩形MNGC的面积S=MN×NG=x($\frac{8a}{3}$-2x),由此能求出当N,E两点重合时,面积最大,并能求出最大面积.
解答 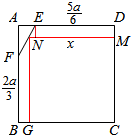 解:由已知得所截矩形样式只有一种,其各边分别与正方开形平行,
解:由已知得所截矩形样式只有一种,其各边分别与正方开形平行,
设矩形一边MN为x($\frac{5a}{6}≤x≤a$),
与NG边的关系为:2(x-$\frac{5a}{6}$)=(a-NG),
∴NG=a-2x+$\frac{5a}{3}$=$\frac{8a}{3}$-2x,
矩形MNGC的面积S=MN×NG=x($\frac{8a}{3}$-2x)=$\frac{8a}{3}$x-2x2=-2(x-$\frac{2a}{3}$)2+$\frac{8{a}^{2}}{9}$,
∴当x=$\frac{2a}{3}$时,面积有极值,但此取值不在限制范围内,
离此最近的点是x=$\frac{5a}{6}$,即N点与E点重合.
∴当N,E两点重合时,面积最大,最大面积为Smax=-2($\frac{5a}{6}$-$\frac{2a}{3}$)2+$\frac{8{a}^{2}}{9}$=$\frac{17{a}^{2}}{18}$.
点评 本题考查矩形最大面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:解答题
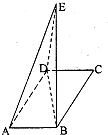 如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.
如图,在平行四边形么BCD中,∠DAB=60°,AD=4,AB=2,将△CBD沿BD折起到△EBD的位置.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com