练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

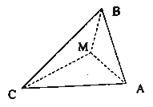
    【题目】在中， ， ， ， 为的中点，将沿折起，使间的距离为，则点到平面的距离为（ ）

    A. B. C. 1 D.

    【答案】A

    【解析】由已知得AB=2,AM=MB=MC=1,BC=，

    由△AMC为等边三角形,取CM中点D,则AD⊥CM,AD交BC于E,则AD=,DE=,CE=.

    折起后,由BC2=AC2+AB2,知∠BAC=90，

    又cos∠ECA=,∴AE2=CA2+CE22CACEcos∠ECA=,于是AC2=AE2+CE2.

    ∴∠AEC=90.

    ∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥ABCM的高,AE=

    设点M到面ABC的距离为h，则

    ∵S△BCM=

    ∴由VABCM=VMABC,可得××=×××1×h,∴h=

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司为确定下一年投入某种产品的宣传费，需了解年宣传费x（单位：千元）对年利润y（单位：万元）的影响，对近5年的宣传费xi和年利润yi（i=1，2，3，4，5）进行了统计，列出了下表：

    x（单位：千元）

    2

    4

    7

    17

    30

    y（单位：万元）

    1

    2

    3

    4

    5

    员工小王和小李分别提供了不同的方案．
    （1）小王准备用线性回归模型拟合y与x的关系，请你建立y关于x的线性回归方程（系数精确到0.01）；
    （2）小李决定选择对数回归模拟拟合y与x的关系，得到了回归方程： =1.450lnx+0.024，并提供了相关指数R2=0.995，请用相关指数说明选择哪个模型更合适，并预测年宣传费为4万元的年利润（精确到0.01）（小王也提供了他的分析数据 （yi﹣ i）2=1.15） 参考公式：相关指数R2=1﹣
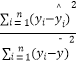
    回归方程 = x+ 中斜率和截距的最小二乘法估计公式分别为 = 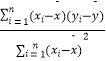， = ﹣ x，参考数据：ln40=3.688， =538．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn ， S4=﹣24，a1+a5=﹣10． （Ⅰ）求{an}的通项公式；
    （Ⅱ）设集合A={n∈N*|Sn≤﹣24}，求集合A中的所有元素．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某科考试中，从甲、乙两个班级各抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图所示，成绩不小于90分为及格． （Ⅰ）设甲、乙两个班所抽取的10名同学成绩方差分别为 、 ，比较 、 的大小（直接写出结果，不写过程）；
    （Ⅱ）从甲班10人任取2人，设这2人中及格的人数为X，求X的分布列和期望；
    （Ⅲ）从两班这20名同学中各抽取一人，在已知有人及格的条件下，求抽到乙班同学不及格的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD，PA⊥AD.E和F分别是CD和PC的中点，求证：

    （1）PA⊥底面ABCD;

    （2）平面BEF⊥平面PCD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图都是边长为1的正方体叠成的几何体，例如第（1）个几何体的表面积为6个平方单位，第（2）个几何体的表面积为18个平方单位，第（3）个几何体的表面积是36个平方单位．依此规律，则第n个几何体的表面积是个平方单位．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB＝5，AA1＝4，点D是AB的中点．

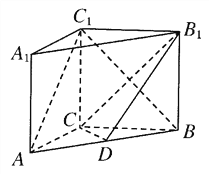
    (1)求证：AC1∥平面CDB1；

    (2)求异面直线AC1与B1C所成角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，初赛采用选手选一题答一题的方式进行，每位选手最多有5次选题答题的机会，选手累计答对3题或答错3题即终止其初赛的比赛，答对3题者直接进入决赛，答错3题者则被淘汰．已知选手甲答题的正确率为 ． （Ⅰ）求选手甲可进入决赛的概率；
    （Ⅱ）设选手甲在初赛中答题的个数为ξ，试写出ξ的分布列，并求ξ的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）= +lg（x﹣1）的定义域是（ ）
    A.（1，+∞）
    B.（﹣∞，2）
    C.（2，+∞）
    D.（1，2]

    查看答案和解析>>

    同步练习册答案