
| A�� | $[{\frac{5}{6}��+��}��$ | B�� | [2��+�ޣ� | C�� | $[{\frac{5}{3}��+��}��$ | D�� | [10��+�ޣ� |
���� ���ú���a�������ڵĶ������μ���f��x���ڸ��������ϵĽ���ʽ������f��x����[n��n+1���ϵĽ���ʽ�����ú����ĵ������г�����ʽ���ɵó�a�ķ�Χ��
��� �⣺��x��[1��2��ʱ��f��x��=2x+1��
�൱x��[2��3��ʱ��f��x��=af��x-1��=a•[2��x-1��+1]��
��
��x��[n��n+1��ʱ��f��x��=af��x-1��=a2f��x-2��=��=an-1f��x-n+1��=an-1•[2��x-n+1��+1]��
��x��[n��n+1��ʱ��f��x��=an-1•[2��x-n+1��+1]��n��N*��
�൱x��[n-1��n��ʱ��f��x��=an-2•[2��x-n+1+1��+1]=an-2•[2��x-n+2��+1]��
��f��x����[1��+�ޣ��ϵ���������
��an-2•5��an-1•3�������
��a��$\frac{5}{3}$��
��ѡC��
���� ���⿼���˺�������ʽ����⣬�ֶκ��������Ե�Ӧ�ã������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��3�� | B�� | 5��4�� | C�� | 9��2�� | D�� | 48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{{\sqrt{3}}}{2}-1$ | B�� | $-\frac{{\sqrt{3}}}{2}+1$ | C�� | $\frac{{\sqrt{3}}}{2}-1$ | D�� | $\frac{{\sqrt{3}}}{2}+1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
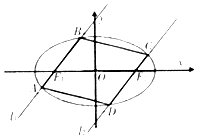 ��ͼ������ԲC��$\frac{{x}^{2}}{4}$+y2=1�����ҽ���F1��F2�ֱ���ֱ��l1��l2����Բ��A��B��C��D����l1��l2��
��ͼ������ԲC��$\frac{{x}^{2}}{4}$+y2=1�����ҽ���F1��F2�ֱ���ֱ��l1��l2����Բ��A��B��C��D����l1��l2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD�������Σ�PA�͵���ABCD��PA=PB��E��F�ֱ���PA��PB���е㣮
��ͼ��������P-ABCD�У�����ABCD�������Σ�PA�͵���ABCD��PA=PB��E��F�ֱ���PA��PB���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com