
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.分析 (1)分别取AD,BC的中点H,G,连接EF、EH、HG、FG,推导出E、F、G、H四点共面,平面FEHG为所求平面α,先求出EH∥面PCD,再求出HG∥面PCD,从而得到α∥面PCD.
(2)设PA=2a,则EF=a,GH=2a,截面α面积为梯形EFGH的面积,推导出梯形EFGH为直角梯形,由此能求出四棱锥P-ABCD的体积.
解答 证明:(1)如图所示,分别取AD,BC的中点H,G,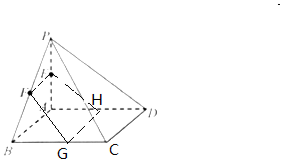
连接EF、EH、HG、FG,
∵EF∥AB,AB∥HG,∴EF∥HG,即E、F、G、H四点共面,
则平面FEHG为所求平面α,
∵EH∥PD,EH?面PCD,PD?面PCD,∴EH∥面PCD.
同理可得:HG∥面PCD,且HG∩EH=H,
∴α∥面PCD.
解:(2)设PA=2a,则EF=a,GH=2a,
由(1)知截面α面积为梯形EFGH的面积,
∵PA⊥面ABCD,AB是PB在平面ABCD的射影,且AB⊥BC,∴PB⊥BC,
同理可证:EH⊥GH,∴梯形EFGH为直角梯形.
在Rt△FBG中,BF=$\sqrt{2}a$,BG=a,∴GH=2a,
∴S梯形EFGH=$\frac{(EF+GH)•EH}{2}$=$\frac{3\sqrt{2}}{2}$,∴a=1,
∴VP-ABCD=$\frac{1}{3}$•PA•S正方形ABCD=$\frac{8}{3}$.
点评 本题考查满足条件的平面的求法,考查四棱锥的体积的求法,考查推理论证能力、运算求解能力、空间想象能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{5}{6},+∞})$ | B. | [2,+∞) | C. | $[{\frac{5}{3},+∞})$ | D. | [10,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
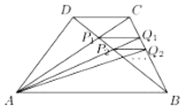 梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)
梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
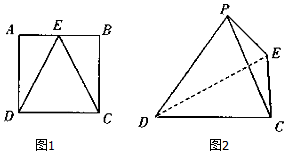 如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
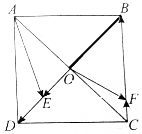
 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的| A. | 100$\sqrt{2}$米 | B. | 50($\sqrt{3}$+1)米 | C. | $100({\sqrt{3}+1})$米 | D. | 200米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com