
 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{2}$ |
分析 根据向量的三角形法则和向量的数乘运算求出λ=$\frac{1}{3}$,μ=$\frac{2}{3}$,再代值计算即可.
解答 解:∵$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{AC}$=$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{AB}$=$\overrightarrow{OA}$+$\frac{2}{3}$($\overrightarrow{OB}$-$\overrightarrow{OA}$)=$\frac{1}{3}$$\overrightarrow{OA}$+$\frac{2}{3}$$\overrightarrow{OB}$,
∴λ=$\frac{1}{3}$,μ=$\frac{2}{3}$,
∴$\frac{1}{λ}$+$\frac{1}{μ}$=3+$\frac{3}{2}$=$\frac{9}{2}$,
故选:D
点评 本题考查了向量的三角形法则和向量的数乘运算,属于基础题.


 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}-1$ | B. | $-\frac{{\sqrt{3}}}{2}+1$ | C. | $\frac{{\sqrt{3}}}{2}-1$ | D. | $\frac{{\sqrt{3}}}{2}+1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥底面ABCD,PA=PB,E,F分别是PA,PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $[{-1,-\frac{2}{3}})∪[5,10)$ | C. | $({-\frac{4}{3},-1}]∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
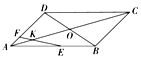 如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{10}{27}$ | D. | $\frac{11}{27}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com