
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $[{-1,-\frac{2}{3}})∪[5,10)$ | C. | $({-\frac{4}{3},-1}]∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
分析 根据[x]的定义,分别作出函数y=f(x)和y=k(x-2)-2的图象,利用数形结合即可得到结论.
解答 解:令F(x)=0得f(x)=k(x-2)-2,
作出函数y=f(x)和y=k(x-2)-2的图象如下图所示:
若函数F(x)=f(x)-k(x-2)+2在(-1,4]上有2个零点,
则函数f(x)和g(x)=k(x-2)-2的图象在(-1,4]上有2个交点,
经计算可得kPA=5,kPB=10,kPO=-1,kPC=-$\frac{2}{3}$,
∴k的范围是[-1,-$\frac{2}{3}$)∪[5,10).
故选:B.
点评 本题考查了对新定义的理解,函数零点的个数与函数图象的关系,数形结合解题思想,属于中档题.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
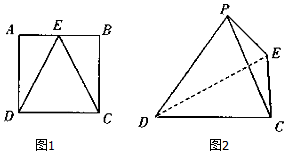 如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.
如图,E是边长为2的正方形ABCD的AB边的中点,将△AED与△BEC分别沿ED、EC折起,使得点A与点B重合,记为点P,得到三棱锥P-CDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
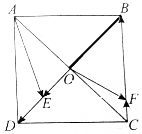
 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{5}{2}$) | B. | [1,$\frac{5}{2}$) | C. | ($\frac{5}{2}$,3) | D. | ($\frac{5}{2}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 29 | B. | 30 | C. | 31 | D. | 33 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的| A. | 100$\sqrt{2}$米 | B. | 50($\sqrt{3}$+1)米 | C. | $100({\sqrt{3}+1})$米 | D. | 200米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com