
���� ��1�������л��ҡ����Ǻ͵����ҹ�ʽ���յ���ʽ������֪��ʽ�ӣ�������ǵ����Ǻ���ֵ���A��
��2���ɣ�1�����ڽǺͶ�����ʾ��C���������ʽ���ö����ǹ�ʽ�����Ǻ�����ʽ����������������г�����ʽ�����B�ķ�Χ�������Һ������������������ֵ��
��3������һ��ѡ��٢ڣ������������Ҷ����г��������b��ֵ�����������ε������ʽ��⼴�ɣ�
��������ѡ��٢ۣ����ڽǺͶ��������Ҷ����ֱ����C��c���������ε������ʽ��⼴�ɣ�
��� �⣺��1��������ã�1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$��
�����Ҷ����ã�1+$\frac{sinAcosB}{cosAsinB}$=$\frac{sin��A+B��}{cosAsinB}$=$\frac{2sinC}{sinB}$��
��cosA=$\frac{1}{2}$����A=$\frac{��}{3}$��
��2����ΪA+B+C=�У�A=$\frac{��}{3}$������B+C=$\frac{2��}{3}$��
��y=2sin2B-2cosBcosC=1-cos2B-2sinBcos��$\frac{2��}{3}$-B��=$\frac{3}{2}$-sin��2B+$\frac{��}{6}$��
�֡�ABCΪ��������Σ���$\frac{��}{6}$��B��$\frac{��}{2}$����$\frac{��}{2}$��2B+$\frac{��}{6}$��$\frac{7��}{6}$������sin��2B+$\frac{��}{6}$���ʣ�-$\frac{1}{2}$��1����
����y�ʣ�$\frac{1}{2}$��2����
��3������һ��ѡ��٢ڣ���ȷ����A BC��
��ΪA=60�㣬a=1��2c-��$\sqrt{3}$+1��b=0��
�����Ҷ����ã�$1={b}^{2}+��\frac{\sqrt{3}+1}{2}b��^{2}-2b•\frac{\sqrt{3}+1}{2}b•\frac{1}{2}$��
�����ã�b2=$\frac{2}{3}$��b=$\frac{\sqrt{6}}{3}$��c=$\frac{\sqrt{6}+3\sqrt{2}}{6}$��
����S��ABC=$\frac{1}{2}•\frac{\sqrt{6}}{3}•\frac{\sqrt{6}+3\sqrt{2}}{6}•\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}+3}{12}$
��������ѡ��٢ۣ���ȷ����A BC��
��Ϊ A=60�㣬B=45�㣬��C=75�㣬
�����Ҷ���b=$\frac{1•sin45��}{sin60��}$=$\frac{\sqrt{6}}{3}$��
����S��ABC=$\frac{1}{2}•1•\frac{\sqrt{6}}{3}•\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{\sqrt{3}+3}{12}$��
���� ���⿼�����Ҷ��������Ҷ������ۺ�Ӧ�ã����Ǻ����Ĺ�ʽ�������ǹ�ʽ��Ӧ�ã��Լ����Һ��������ʣ�ע����ǽǵķ�Χ�����黯���������������е��⣮


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�0�� | B�� | ��-�ޣ�0] | C�� | [2��+�ޣ� | D�� | ��2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
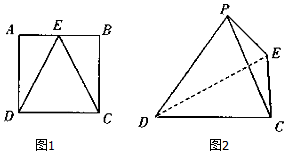 ��ͼ��E�DZ߳�Ϊ2��������ABCD��AB�ߵ��е㣬����AED���BEC�ֱ���ED��EC����ʹ�õ�A���B�غϣ���Ϊ��P���õ�����P-CDE��
��ͼ��E�DZ߳�Ϊ2��������ABCD��AB�ߵ��е㣬����AED���BEC�ֱ���ED��EC����ʹ�õ�A���B�غϣ���Ϊ��P���õ�����P-CDE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ���ı���ABCD�У�M��N�ֱ�ΪAB��AD�ϵĵ㣬��$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$������AC��MN����P�㣬��$\overrightarrow{AP}$=��$\overrightarrow{AC}$����˵�ֵΪ��������
��ͼ����ƽ���ı���ABCD�У�M��N�ֱ�ΪAB��AD�ϵĵ㣬��$\overrightarrow{AM}$=$\frac{4}{5}$$\overrightarrow{AB}$��$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AD}$������AC��MN����P�㣬��$\overrightarrow{AP}$=��$\overrightarrow{AC}$����˵�ֵΪ��������| A�� | $\frac{3}{5}$ | B�� | $\frac{3}{7}$ | C�� | $\frac{4}{11}$ | D�� | $\frac{4}{13}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��OAB������C����$\overrightarrow{AC}=2\overrightarrow{CB}��\overrightarrow{OC}=��\overrightarrow{OA}+��\overrightarrow{OB}���ˣ��̡�R��$����$\frac{1}{��}+\frac{1}{��}$=
��ͼ����֪��OAB������C����$\overrightarrow{AC}=2\overrightarrow{CB}��\overrightarrow{OC}=��\overrightarrow{OA}+��\overrightarrow{OB}���ˣ��̡�R��$����$\frac{1}{��}+\frac{1}{��}$=| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{3}$ | C�� | $\frac{2}{9}$ | D�� | $\frac{9}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 29 | B�� | 30 | C�� | 31 | D�� | 33 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com