
设椭圆C:  +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为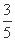 .
.
(1)求C的方程;
(2)求过点(3,0)且斜率为 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标.
科目:高中数学 来源: 题型:
已知向量a=(sin θ,cos θ),b=(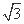 ,1),其中θ∈(0,
,1),其中θ∈(0, 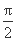 ).
).
(1)若a∥b,求sin θ和cos θ的值;
(2)若f(θ)=(a+b)2,求f(θ)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
双曲线的中心在坐标原点O,A、C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F是双曲线的左焦点,直线AB与FC相交于点D,若双曲线的离心率为2,则∠BDF的余弦值是( )
(A)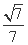 (B)
(B)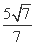 (C)
(C)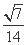 (D)
(D)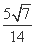
查看答案和解析>>
科目:高中数学 来源: 题型:
设F1,F2是椭圆E:  +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
(A) (B)
(B) (C)
(C) (D)
(D) 
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆C:  +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P(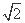 ,
, ).
).
(1)求椭圆C的方程;
(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点.过点Q作x轴的垂线,垂足为E.取点A(0,2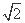 ),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知A,B分别为椭圆 +
+ =1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )

(A)± (B)±
(B)±
(C)± (D)±
(D)±
查看答案和解析>>
科目:高中数学 来源: 题型:
某市为增强市民的节约粮食意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.若用分层抽样的方法从第3,4,5组中共抽取了12名志愿者参加10月16日的“世界粮食日”宣传活动,则从第4组中抽取的人数为________人.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com