练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．解下列关于x的不等式：
    （1）-x2+2x+1＜0
    （2）$\frac{3x+3}{x}≤2$．

    分析 （1）将二次项系数化为正数，然后解之；
    （2）移项通分，等价转化为整式不等式解之．

    解答 解：（1）$-{x^2}+2x+1＜0?{x^2}-2x-1＞0?x＜1-\sqrt{2}或x＞1+\sqrt{2}$
    所以不等式的解集是$（{-∞，1-\sqrt{2}}）∪（{1+\sqrt{2}，+∞}）$；
    （2）$\frac{3x+3}{x}≤2?\frac{3x+3}{x}-2≤0?\frac{x+3}{x}≤0$$?\left\{\begin{array}{l}x≠0\\ x（{x+3}）≤0\end{array}\right.?-3≤x＜0$，所以不等式的解集是[-3，0）．

    点评 不同考查了不等式的解法；关键是等价转化为最简的整式不等式解之．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

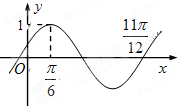    3．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$|的部分图象如图示，现将函数y=f（x）的图象向右平移$\frac{π}{12}$个单位后，得到函数y=g（x）的图象，则平移后得到的函数解析式g（x）=sin2x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．解关于x的不等式4≤x2-3x-6≤2x+8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=m（m≠0）$的渐近线斜率为±2，则该双曲线的离心率为（　　）
    A．$\sqrt{3}$B．$\sqrt{5}$C．$\sqrt{5}$或$\frac{{\sqrt{5}}}{2}$D．$\sqrt{3}$或$\frac{{2\sqrt{3}}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知数列{an}中，a1=-$\frac{1}{4}$，an=1-$\frac{1}{{a}_{n-1}}$（n＞1），则a2016的值为（　　）
    A．-$\frac{1}{4}$B．5C．$\frac{4}{5}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=（x-t）|x|（t∈R）．
    （1）讨论y=f（x）的奇偶性；
    （2）当t＞0时，求f（x）在区间[-1，2]的最小值h（t）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数$f（x）=\frac{{{2^{x+1}}}}{{{2^x}+1}}$．
    （1）求证：函数f（x）在实数集R上为增函数；
    （2）设g（x）=log2f（x），若关于x的方程g（x）=a有解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．当x＞1时不等式$\frac{{{x^2}-x+1}}{x-1}≥a$恒成立，则实数a的取值范围是（　　）
    A．（-∞，3]B．[3，+∞）C．（-∞，2]D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=$\frac{x}{1+x}$．
    （1）画出f（x）的草图；
    （2）指出f（x）的单调区间．

    查看答案和解析>>

    同步练习册答案