
分析 设$g(x)=f(x)-\frac{1}{x}-4$对其求导,结合已知不等式得到其单调性,所求不等式转利用单调性得到自变量的大小,即x范围.
解答 解:由x2f′(x)+1>0,设$g(x)=f(x)-\frac{1}{x}-4$,则$g′(x)=f′(x)+\frac{1}{x^2}$=$\frac{{x}^{2}f'(x)+1}{{x}^{2}}$>0.
故函数g(x)在(0,+∞)上单调递增,又g(1)=0,故g(x)<0的解集为(0,1),
即$f(x)<\frac{1}{x}-4$的解集为(0,1).
故答案为:(0,1).
点评 本题考查了抽象不等式的解法;关键是正确构造新函数,利用已知不等式得到函数的单调性.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 2 | C. | 1 | D. | $\sqrt{3}+\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -14 | B. | -28 | C. | 14 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
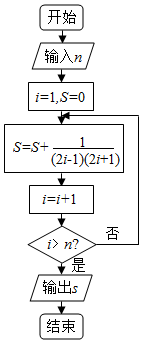
| A. | $\frac{4}{9}$ | B. | $\frac{8}{9}$ | C. | $\frac{5}{11}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com