
分析 当AB的长度最小时,圆心角∠ACB 最小,设为2$\theta$,当$\theta$ 最小时,$cos\theta$ 最大,即CM 最小,由此能求出直线AB的方程.
解答  解:当AB的长度最小时,圆心角∠ACB 最小,设为2$\theta$
解:当AB的长度最小时,圆心角∠ACB 最小,设为2$\theta$
则由$cosθ=\frac{AC}{CM}=\frac{1}{CM}$,
知当$\theta$ 最小时,$cos\theta$ 最大,即CM 最小,那么CM⊥l,
∴${k_{AB}}={k_l}=-\frac{3}{4}$,
设直线AB的方程为3x+4y=m.
又由CM=2,知点C 到直线AB的距离为$\frac{1}{2}$,
即$\frac{1}{2}=\frac{{|{3+4-m}|}}{5}$,解得$m=\frac{19}{2}$ 或m=$\frac{9}{2}$;
经检验$m=\frac{19}{2}$,则直线AB的方程为6x+8y-19=0.
故答案为:6x+8y-19=0.
点评 本题考查直线方程的求法,是中档题,解题时要认真审题,注意圆的性质、三角函数知识的合理运用.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
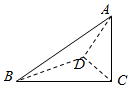 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=2$\sqrt{5}$,BD=2,CD=$\sqrt{3}$,则球O的体积为( )
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BD⊥AD,且AD=2$\sqrt{5}$,BD=2,CD=$\sqrt{3}$,则球O的体积为( )| A. | 8$\sqrt{6}$π | B. | $\frac{27\sqrt{3}π}{2}$ | C. | $\frac{7\sqrt{7}π}{6}$ | D. | 10$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com