
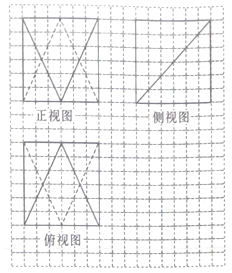
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )| A. | 72 | B. | $90\sqrt{3}$ | C. | $108\sqrt{2}$ | D. | 144 |
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | ($\frac{3}{2}$,4) | B. | ($\frac{3}{2}$,2) | C. | (1,4) | D. | (2,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x3 | B. | y=2x3-x2 | C. | y=2x3+x2 | D. | y=x5-x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$•($\frac{1}{2}$)n-1 | B. | $\frac{3}{2}•{({-\frac{1}{2}})^{n-2}}$ | C. | $\frac{3}{2}$•(-$\frac{1}{2}$)n-2 | D. | $\frac{3}{2}$•(-2)n-1或$\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,loga3) | C. | (0,+∞) | D. | (loga3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
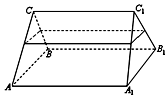 如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )
如图,一个三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点.则当底面ABC水平放置时,液面高为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com