
| A. | 3 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
分析 由s=4πR2=16,得球半径R=2,如图设BC=m,则AB=2m,设O1是△BCD的中心,O是球心,则BO1=$\frac{\sqrt{3}}{3}m$,过O作OH⊥AB于H,则H为AB中点,OO1=HB=m,在直角三角形OO1B中,OO12+BO12=OB2,
解得m即可.
解答 解:由s=4πR2=16,得球半径R=2,
如图设BC=m,则AB=2m,
设O1是△BCD的中心,O是球心,则BO1=$\frac{\sqrt{3}}{3}m$,
过O作OH⊥AB于H,则H为AB中点,∴OO1=HB=m,
在直角三角形OO1B中,OO12+BO12=OB2,
m2+$\frac{1}{3}{m}^{2}=4$,解得m=$\sqrt{3}$,
∵△BCD的面积为$\frac{1}{2}×\sqrt{3}×\sqrt{3}×\frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}$,AB=2m=2$\sqrt{3}$,
三棱锥B-ACD的体积为v=$\frac{1}{3}×{s}_{△BCD}×AB=\frac{3}{2}$.
故选:C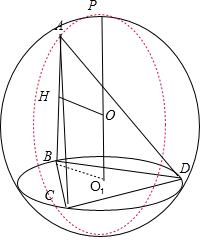
点评 本题考查了球与三棱锥的组合体,关键是找准相应位置关系.属于中档题


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | ? | B. | 0 | C. | {0} | D. | {-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 对服务满意 | 对服务不满意 | 合计 | |
| 对商品满意 | 80 | ||
| 对商品不满意 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
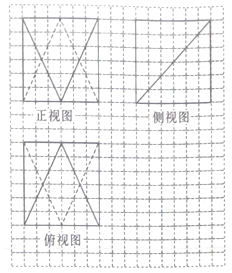 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某个多面体的三视图,则该多面体的体积为( )| A. | 72 | B. | $90\sqrt{3}$ | C. | $108\sqrt{2}$ | D. | 144 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com