
【题目】已知函数f(x)的定义域为(﹣1,1),且同时满足下列条件:f(1﹣a)+f(1﹣a2)<0.求a的取值范围.
【答案】解:由f(1﹣a)+f(1﹣a2)<0得f(1﹣a)<﹣f(1﹣a2),
∵函数y=f(x)是奇函数,
∴﹣f(1﹣a2)=f(a2﹣1),
即不等式等价为f(1﹣a)<f(a2﹣1),
∵y=f(x)在定义域(﹣1,1)上是减函数,
∴有 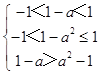 ,即
,即 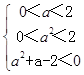 ,
,
∴ 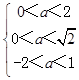 ,解得0<a<1
,解得0<a<1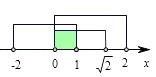
【解析】利用函数是奇函数,将不等式f(1﹣a)+f(1﹣a2)<0转化为f(1﹣a)<﹣f(1﹣a2)=f(a2﹣1),然后利用函数的单调性进行求解.
【考点精析】关于本题考查的函数单调性的判断方法和函数的奇偶性,需要了解单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称才能得出正确答案.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC= ![]() ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点. 
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax3﹣3x+1 对于x∈[﹣1,1]总有f(x)≥0成立,则a 的取值范围为( )
A.[2,+∞)
B.[4,+∞)
C.{4}
D.[2,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 ![]() ,
, ![]()
(1)分别求出小球落入A袋和B袋中的概率;
(2)在容器 入口处依次放入4个小球,记ξ为落入B袋中的小球个数,求ξ的分布列和数学期望.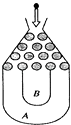
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出最小二乘法下的回归直线方程 ![]() =
= ![]() x+
x+ ![]() 系数公式:
系数公式: ![]() =
= 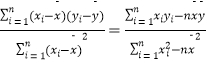 ,
, ![]()
假设关于某设备的使用年限x(年)和所支出的维修费用y(万元),有如表的统计资料:
使用年限x (年) | 2 | 3 | 4 | 5 | 6 |
维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料可知y对x呈线性相关关系,试求:
(1)线性回归直线方程;
(2)根据回归直线方程,估计使用年限为12年时,维修费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com