练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】对于任意实数x，函数f（x）=（5﹣a）x2﹣6x+a+5恒为正值，求a的取值范围．

    【答案】解：由函数f（x）=（5﹣a）x2﹣6x+a+5恒为正值，
    若5﹣a=0，即a=5时，不等式等价为﹣6x+10＞0，此时不满足条件．
    ∴a≠5，
    要使函数f（x）=（5﹣a）x2﹣6x+a+5恒为正值，
    则 ，
    解得﹣4＜a＜4，
    ∴a的取值范围是﹣4＜a＜4
    【解析】函数f（x）=（5﹣a）x2﹣6x+a+5恒为正值，可转化为5﹣a＞0，且△＜0，解不等式组可得答案．
    【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在Rt△AOB中，∠OAB= ，斜边AB=4．Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到，且二面角B﹣AO﹣C是直二面角，动点D在斜边AB上．
    （Ⅰ）求证：平面COD⊥平面AOB；
    （Ⅱ）当VA﹣DOC：VA﹣BOC=1：2时，求CD与平面AOB所成角的大小．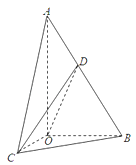

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论在上的单调性；

    （2）是否存在实数，使得在上的最大值为，若存在，求满足条件的的个数；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥中， ， 底面， ，且.

    （1）若为上一点，且，证明:平面平面.

    （2）若为棱上一点，且平面，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知随机变量X服从正态分布N（μ，σ2），且P（μ﹣2σ＜X＜μ+2σ）=0.954 4，P（μ﹣σ＜X＜μ+σ）=0.6826．若μ=4，σ=1，则P（5＜X＜6）=（ ）
    A.0.1359
    B.0.1358
    C.0.2718
    D.0.2716

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）的定义域为（﹣1，1），且同时满足下列条件：f（1﹣a）+f（1﹣a2）＜0．求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程为，其中为参数， ，再以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为，其中， ，直线与曲线交于两点.

    （1）求的值；

    （2）已知点，且，求直线的普通方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥V﹣ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC= ，O，M分别为AB，VA的中点．

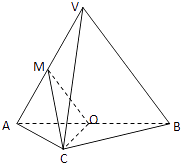
    （1）求证：VB∥平面MOC．
    （2）求证：平面MOC⊥平面VAB．
    （3）求二面角C﹣VB﹣A的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有4名男生，3名女生排成一排：
    （1）从中选出3人排成一排，有多少种排法？
    （2）若男生甲不站排头，女生乙不站在排尾，则有多少种不同的排法？
    （3）要求女生必须站在一起，则有多少种不同的排法？
    （4）若3名女生互不相邻，则有多少种不同的排法？

    查看答案和解析>>

    同步练习册答案