
【题目】已知随机变量X服从正态分布N(μ,σ2),且P(μ﹣2σ<X<μ+2σ)=0.954 4,P(μ﹣σ<X<μ+σ)=0.6826.若μ=4,σ=1,则P(5<X<6)=( )
A.0.1359
B.0.1358
C.0.2718
D.0.2716
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
【题目】根据《中华人民共和国道路交通安全法》规定:“车辆驾驶员血液酒精溶度(单位mg/100ml)/在![]() ,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
,属于酒后驾驶;血液浓度不低于80,属于醉酒驾驶。”2017年“中秋节”晚9点开始,济南市交警队在杆石桥交通岗前设点,对过往的车辆进行检查,经过4个小时,共查处喝过酒的驾驶者60名,下图是用酒精测试仪对这60名驾驶者血液中酒精溶度进行检测后所得结果画出的频率分布直方图。
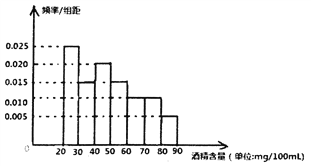
(1)求这60名驾驶者中属于醉酒驾车的人数(图中每组包括左端点,不包括右端点)
(2)若以各小组的中值为该组的估计值,频率为概率的估计值,求这60名驾驶者血液的酒精浓度的平均值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆M:: ![]() +
+ ![]() =1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
=1(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,计算得 ![]() =80,
=80, ![]() =20,
=20, ![]() i=184,
i=184, ![]() =720.
=720.
(1)求家庭的月储蓄对月收入的回归方程;
(2)判断月收入与月储蓄之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C过点A(6,4),B(1,﹣1),且圆心在直线l:x﹣5y+7=0上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com