练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．不等式|x+1|-|x-5|＜4的解集为（　　）
    A．（-∞，4）B．（-∞，-4）C．（4，+∞）D．（-4，+∞）

    分析 通过讨论x的范围，求出各个阶段上的x的范围，取并集即可．

    解答 解：x≥5时：
    x+1-x+5=6＞4，不等式无解；
    -1＜x＜5时：
    x+1+x-5＜4，解得：x＜4；
    x≤-1时：
    -x-1+x-5＜4恒成立．
    故不等式的解集是（-∞，4）．

    点评 本题考查了绝对值不等式问题，考查分类讨论思想，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=Asin2（ωx+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象经过最高点（1，2），且相邻两对称轴间的距离为2．
    （1）求函数f（x）的表达式；
    （2）若函数g（x）=f（x）+f（1-x），x∈[-3，3]，求使得g（t）=3成立的实数t的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．函数f（x）=$\left\{\begin{array}{l}{\frac{1}{2}x-1，x≥0}\\{\frac{1}{x}，x＜0}\end{array}\right.$，若f（a）≤a，则实数a的取值范围是a≥-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知函数f（x）=ax+$\frac{a-1}{x}$+（1-2a）（a＞0）
    （1）若f（x）≥lnx在[1，+∞）上恒成立，求a的取值范围；
    （2）证明：1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＞ln（n+1）+$\frac{n}{2（n+1）}$（n≥1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．如图所示，在直角梯形ABCD中，AB∥CD，∠BCD=90°，BC=CD=2，AF=BF，EC∥FD，FD⊥底面ABCD，M是AB的中点．
    （1）求证：平面CFM⊥平面BDF；
    （2）点N在CE上，EC=2，FD=3，当CN为何值时，MN∥平面BEF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．为了增强环保意识，某校从男生中随机制取了60人，从女生中随机制取了50人参加环保知识测试，统计数据如表所示，经计算K2=7.822，则环保知识是否优秀与性别有关的把握为（　　）
    优秀非优秀总计
    男生402060
    女生203050
    总计6050110
    附：x2=$\frac{n（{n}_{11}{n}_{22}-{n}_{12}{n}_{21}）^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}{n}_{+2}}$
    P（K2≥k）0.5000.1000.0500.0100.001
    k0.4552.7063.8416.63510.828
    A．90%B．95%C．99%D．99.9%

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．等比数列{an}的前n项和为Sn，已知S4=a2+a3+9a1，a5=32，则a1=（　　）
    A．-$\frac{1}{2}$B．$\frac{1}{2}$C．2D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知函数f（x）=$\left\{\begin{array}{l}-{x^2}+2x，x≤0\\ ln（x+1），x＞0\end{array}\right.$，若对x∈R都有|f（x）|≥ax，则实数a的取值范围是（　　）
    A．（-∞，0]B．[-2，0]C．[-2，1]D．（-∞，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

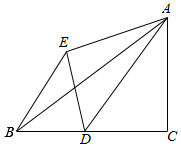    6．如图，△ABC中，∠C=90°，AC=6，BC=8，点D从点C出发，以每秒1个单位的速度沿着CB向点B运功，△ADE和△ADC关于AD成轴对称，连接BE，设点D运动时间为t秒．
    （1）当t为何值时，△BDE是以BE为底的等腰三角形？
    （2）当t为何值时，用BD，DE、AD的长度作为线段所围成的三角形是以BD为直角边的直角三角形？

    查看答案和解析>>

    同步练习册答案