
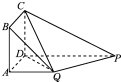
 四边形ABCD为正方形,BA⊥面ADPQ,AD⊥AQ,PD∥AQ,
四边形ABCD为正方形,BA⊥面ADPQ,AD⊥AQ,PD∥AQ,分析 (1)由AD⊥DP,CD⊥平面ADPQ,可得DA,DP,DC两两垂直.以D为原点,DA,DP,DC所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz.利用向量垂直与数量积的关系即可得出.
(2)利用棱锥的体积计算公式即可得出.
解答 (1)证明:∵AD⊥DP,CD⊥平面ADPQ,∴DA,DP,DC两两垂直.以D为原点,
DA,DP,DC所在直线为x轴,y轴,z轴建立空间直角坐标系D-xyz.
不妨设AB=1,则D(0,0,0),B(1,0,1),
C(0,0,1),Q(1,1,0),P(0,2,0).
$\overrightarrow{PQ}$=(1,-1,0),
$\overrightarrow{PQ}$$•\overrightarrow{DQ}$=1-1+0=0,∵BA⊥面ADPQ,BA∥DC,
∴DC⊥面ADPQ,∴DC⊥PQ.
∴DC⊥PQ,DQ⊥PQ,又DC∩DQ=D,
∴PQ⊥平面DCQ.
(2)解:设AB=a,由题设,QA⊥AD,QA⊥CD,知AQ为棱锥Q-ABCD的高,
∴棱锥Q一ABCD的体积V1=$\frac{1}{3}{a}^{3}$,
棱锥P-DCQ的体积V2=VC-DPQ=$\frac{1}{3}$a•$\frac{1}{2}$•3a•a=$\frac{1}{2}{a}^{3}$,
故棱锥Q-ABCD的体积:棱锥P-DCQ的体积=2:3.
点评 本题考查了线面垂直的判定与性质定理、棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${A}_{27-a}^{8}$ | B. | $A_{34-a}^{27-a}$ | C. | $A_{34-a}^7$ | D. | $A_{34-a}^8$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(π)>f(-3.14)>f(-1) | B. | f(π)>f(-1)>f(-3.14) | C. | f(π)=f(-3.14)<f(-1) | D. | f(π)<f(-1)<f(-3.14) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com