练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在某次诗词大会决赛前，甲、乙、丙丁四位选手有机会问鼎冠军，三名诗词爱好者依据选手在之前比赛中的表现，结合自己的判断，对本场比赛的冠军进行了如下猜测：猜测冠军是乙或丁；猜测冠军一定不是丙和丁；猜测冠军是甲或乙。比赛结束后发现，三个人中只有一个人的猜测是正确的，则冠军是（ ）

    A. 甲B. 乙C. 丙D. 丁

    【答案】D

    【解析】

    分别假设甲、乙、丙和丁是冠军，推出矛盾和正确的结果，即可求解，得到答案．

    由题意，选项A中，若甲是冠军，则B和C猜测正确，A猜测错误，不满足题意；

    选项B中，若乙是冠军，则A、B、C猜测都正确，不满足题意；

    选项C中，若丙是冠军，则A、B、C猜测都不正确，不满足题意；

    选项D中，若丁是冠军，则A猜测正确，B和C猜测错误，满足题意，

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数（）的图象为， 关于点的对称的图象为， 对应的函数为．

    （Ⅰ）求函数的解析式，并确定其定义域；

    （Ⅱ）若直线与只有一个交点，求的值，并求出交点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】郑州一中社团为调查学生学习围棋的情况，随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图：将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.

    （1）根据已知条件完成下面的2×2列联表，并据此资料你是否认为“围棋迷”与性别有关？

    非围棋迷

    围棋迷

    合计

    男

    女

    10

    55

    合计

    （2）将上述调查所得到的频率视为概率.现在从该地区大量学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名学生中的“围棋迷”人数为.若每次抽取的结果是相互独立的，求的分布列，期望

    附：,

    0.05

    0.01

    3.841

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设，用表示不超过x的最大整数，则称为高斯函数，例如：，.已知函数，则关于函数的叙述中正确的是（ ）

    A.是偶函数B.是奇函数

    C.在R上是增函数D.的值域是

    E.的值域是

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体 中， 分别为 的中点，点 是底面内一点，且 平面 ，则 的最大值是( )

    A. B. 2 C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于曲线C：，给出下列五个命题：

    ①曲线C关于直线y=x对称；

    ②曲线C关于点对称；

    ③曲线C上的点到原点距离的最小值为；

    ④当时，曲线C上所有点处的切线斜率为负数；

    ⑤曲线C与两坐标轴所围成图形的面积是.

    上述命题中，为真命题的是_____.（将所有真命题的编号填在横线上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

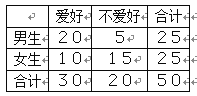
    【题目】通过随机询问50名性别不同的大学生是否爱好某项运动，得到如下的列联表，由得

    参照附表，得到的正确结论是

    　　

    A. 有99.5％以上的把握认为“爱好该项运动与性别有关”

    B. 有99.5％以上的把握认为“爱好该项运动与性别无关”

    C. 在犯错误的概率不超过0．1％的前提下，认为“爱好该项运动与性别有关”

    D. 在犯错误的概率不超过0．1％的前提下，认为“爱好该项运动与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了了解四川省各景点在大众中的熟知度，随机对岁的人群抽样了人，回答问题“四川省有哪几个著名的旅游景点？”统计结果如表．

    组号

    分组

    回答正确的人数

    回答正确的人数

    占本组的频率

    第组

    第组

    第组

    第组

    第组

    （1）分别求出的值；

    （2）从第，，组回答正确的人中用分层抽样的方法抽取人，求第，，组每组各抽取多少人？

    （3）通过直方图求出年龄的众数，平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5]分成9组，制成了如图所示的频率分布直方图.

    （Ⅰ）求直方图中a的值；

    （Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

    （Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

    查看答案和解析>>

    同步练习册答案